Пән үш модулден тұрады: кездейсоқ оқиғалар, кездейсоқ шамалар және математикалық статистика.
Барлық модулдердің жалпы құрылымы бірдей:
1. Әрбір модуль блоктарға бөлінген;
2. Әрбір блок сабақтарға бөлінген;
3. Әрбір сабақ бойынша теориялық материалдар берілген;
4. Әрбір тақырып бойынша есептер шығару үлгілері көрсетілген;
5. Жиі қолданыстағы формулалар;
6. Әрбір сабақ, блок, бөлім және курс бойынша білімді тексеру мүмкіндігі ұсынылады;
7. Қысқаша тарихи мағлұматтар берілген; Авторлар
 I-ші Модуль. Кездейсоқ оқиғалар:
I-ші Модуль. Кездейсоқ оқиғалар:I МОДУЛЬ
КЕЗДЕЙСОҚ ОҚИҒАЛАР
I-блок. Кездейсоқ оқиғалар түрлері. Ықтималдықтың классикалық анықтамасы
1-сабақ. Кездейсоқ оқиғалардың түрлері
Анықтама. Тәжірибе нәтижесінде пайда болған әрбір деректі оқиға деп атайды.
Тәжірибе нәтижесінде пайда болуы да, пайда болмауы да мүмкін оқиға кездейсоқ оқиға деп аталады.
Кездейсоқ оқиғалардың мысалдары:
- теңге лақтыру тәжірибесінде елтаңбаның немесе сан жазылған жағының пайда болуы;
- лотерея ойынында белгілі бір билетке ұтыс шығуы;
- ойнау дәрежелері бірдей екі футбол командасының кездесуінің нәтижесі, т.с.с.
 Кездейсоқ оқиғаларды А, В, С, ... әріптерімен белгілейді.
Кездейсоқ оқиғаларды А, В, С, ... әріптерімен белгілейді.
Тәжірибе нәтижесінде міндетті түрде пайда болатын оқиғаны ақиқат оқиға деп атайды. Мысалы: А- ойын кубын лақтырғанда бүтін санның пайда болуы; егер жәшікке 10 бірдей қызыл шарлар салынса, онда В- жәшіктен қызыл шар алу; С- суға лақтырылған тас батады, т.с.с. Мұнда А, В, С оқиғалары ақиқат оқиғалар болып табылады. Ақиқат оқиға, әдетте, И әрпі арқылы белгіленеді.
Тәжірибе нәтижесінде пайда болмайтын оқиғаны мүмкін емес оқиға деп атайды. Мысалы: А- ойын кубын лақтырғанда 7 ұпай пайда болуы; В- жәшікке ылғи көк шарлар салынғанда, ақ шар пайда болуы; С- туған күніңе ұшатын крокодил сыйлауы, т.с.с. Мұнда А, В, С оқиғалары мүмкін емес оқиғалар болып табылады. Мүмкін емес оқиға, әдетте, V әрпі арқылы белгіленеді.
Тәжірибе нәтижесінде әртүрлі екі А және В оқиғалары бірге пайда бола алмаса, онда олар үйлесімсіз деп аталады, ал егер бірге пайда бола алса, онда олар үйлесімді оқиғалар деп аталады. Мысалы: ойын кубын лақтырғанда ![]() оқиғалары сәйкес 1,2,...,6 сандарының пайда болуын білдірсе, онда бұл оқиғалар үйлесімсіз оқиғалар болып табылады. Ал, егер В- ойын кубын лақтырғанда жұп ұпайдың пайда болуын білдірсе, онда
оқиғалары сәйкес 1,2,...,6 сандарының пайда болуын білдірсе, онда бұл оқиғалар үйлесімсіз оқиғалар болып табылады. Ал, егер В- ойын кубын лақтырғанда жұп ұпайдың пайда болуын білдірсе, онда ![]() және В,
және В, ![]() және В,
және В, 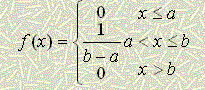 және В үйлесімді оқиғалар болып табылады.
және В үйлесімді оқиғалар болып табылады.
Тәжірибе нәтижесінде 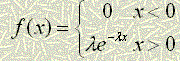 оқиғаларының ең болмағанда біреуі пайда болса, онда бұл оқиғалар толық топ құрады деп айтады. Мысалы: ойын кубын лақтырғанда
оқиғаларының ең болмағанда біреуі пайда болса, онда бұл оқиғалар толық топ құрады деп айтады. Мысалы: ойын кубын лақтырғанда ![]() оқиғаларының біреуі міндетті түрде пайда болады. Демек,
оқиғаларының біреуі міндетті түрде пайда болады. Демек, ![]() оқиғалары толық топ құрады.
оқиғалары толық топ құрады.
 Өзара үйлесімсіз, толық топ құратын екі оқиға қарама-қарсы оқиғалар деп аталады. Мысалы: теңге лақтыру тәжірибесінде
Өзара үйлесімсіз, толық топ құратын екі оқиға қарама-қарсы оқиғалар деп аталады. Мысалы: теңге лақтыру тәжірибесінде ![]() – елтаңбаның пайда болуы,
– елтаңбаның пайда болуы, ![]() - санның пайда болуы болса, онда
- санның пайда болуы болса, онда ![]() ,
, ![]() толық топ құрады. Себебі тәжірибе нәтижесінде олардың біреуі міндетті түрде пайда болады. Сондай-ақ олар үйлесімсіз. Демек,
толық топ құрады. Себебі тәжірибе нәтижесінде олардың біреуі міндетті түрде пайда болады. Сондай-ақ олар үйлесімсіз. Демек, ![]() және
және ![]() қарама-қарсы оқиғалар. Әдетте, А-ға қарама-қарсы оқиға
қарама-қарсы оқиғалар. Әдетте, А-ға қарама-қарсы оқиға ![]() арқылы белгіленеді.
арқылы белгіленеді.
А және В оқиғаларының біреуінің пайда болуы екіншісінің пайда болуына немесе пайда болмауына әсер етпесе, онда олар өзара тәуелсіз оқиғалар деп аталады және А*В арқылы белгіленеді. А және В оқиғаларының көбейтіндісі деп осы екі оқиғалардың бірге пайда болуын айтады. Мысалы: ойын кубын лақтыру тәжірибесінде А-екі санына еселі санның пайда болуы, ал В- үш санына еселі санның пайда болуы, сондай-ақ С- алты санның пайда болуы болсын. Сонда С=А*В екені айқын. Себебі С оқиғасы пайда болса, онда А-да пайда болады және В-да пайда болады.
А және В оқиғаларының қосындысы деп, не А, не В, немесе А және В оқиғаларының пайда болуын айтады. Алдыңғы мысалда А+В оқиғасы 2,3,4,6 сандарының біреуінің пайда болуын білдіреді.
Егер А және В үйлесімсіз болса, онда А+В оқиғасы не А-ның, не В-ның пайда болуын білдіреді.
2-сабақ. Ықтималдықтардың классикалық және статистикалық
анықтамалары
Әдетте, екі оқиғаның пайда болуын салыстырғанда, олардың пайда болу мүмкіндіктері әртүрлі болатыны байқалады. Мысалы, урнада 17 қара 3 көк бірдей шарлар болсын. Белгілеу енгізейік. А- урнада көк шар алынуы, В- қара шар алынуы. Сонда В оқиғасының пайда болу мүмкіндігі А оқиғасының пайда болу мүмкіндігінен жоғары екені байқалады. Себебі урнада қара шарлар саны көп. Осыдан оқиғаның пайда болу мүмкіндігін сипаттайтын сандық шама енгізу қажеттігі туындайды. Осы санды оқиғаның ықтималдығы деп аталады.
Егер бір тәжірибеде екі оқиғаның пайда болу мүмкіндіктері бірдей болса, ондай оқиғалар теңмүмкіндікті оқиғалар деп аталады. Егер урнада 10 қызыл және 10 көк бірдей шарлар болса, А- қызыл шар алу, В- көк шар алу оқиғалары теңмүмкіндікті оқиғалар болып табылады.
Айталық тәжірибе нәтижесінде өзара үйлесімсіз, теңмүмкіндікті және толық топ құратын ![]() оқиғалары пайда болатын болсын. Осындай оқиғаларды элементарлық оқиғалар деп атайды. Тәжірибе нәтижесінде пайда бола алатын А оқиғасы осы тәжірибенің элементарлық оқиғаларының кейбіреуінің қосындысы ретінде өрнектелетін болсын.
оқиғалары пайда болатын болсын. Осындай оқиғаларды элементарлық оқиғалар деп атайды. Тәжірибе нәтижесінде пайда бола алатын А оқиғасы осы тәжірибенің элементарлық оқиғаларының кейбіреуінің қосындысы ретінде өрнектелетін болсын.
 Қосындылары А оқиғасына тең болатын элементарлық оқиғаларды А оқиғасына қолайлы элементарлық оқиғалар деп атайды.
Қосындылары А оқиғасына тең болатын элементарлық оқиғаларды А оқиғасына қолайлы элементарлық оқиғалар деп атайды.
Анықтама (ықтималдықтың классикалық анықтамасы). Тәжірибедегі А оқиғасына қолайлы элементарлық оқиғалар санының осы тәжірибедегі барлық элементарлық оқиғалар санына қатынасын А оқиғасының ықтималдығы деп атайды.
Айталық тәжірибедегі А оқиғасына қолайлы элементарлық оқиғалар саны m, ал барлық элементарлық оқиғалар саны n болсын. Сонда:
.gif)
Мысал 1. Ойын кубы лақтырылсын. Мұнда ![]() - элементарлық оқиғалары сәйкес 1,2,...,6 сандарының пайда болуын білдіреді. А- жұп санның пайда болуы болмын. Сонда
- элементарлық оқиғалары сәйкес 1,2,...,6 сандарының пайда болуын білдіреді. А- жұп санның пайда болуы болмын. Сонда ![]() . демек, А-ға үш элементарлық оқиға қолайлы, яғни =3, ал n=6. Олай болса:
. демек, А-ға үш элементарлық оқиға қолайлы, яғни =3, ал n=6. Олай болса:
![]()
Ықтималдықтың классикалық анықтамасынан:
1. 0≤ P(A)≤1,
2. P(u)=1,
3. P(v)=0
екенін байқауға болады.
Көпшілік жағдайда тәжірибенің нәтижесін элементарлық оқиғалардың қосындысы ретінде өрнектеу қиын болады.Сондықтан оқиғаның ықтималдығының классикалық анықтамасымен қатар статистикалық анықтамасын да қолданады.
Айталық n сынақ жүргізілсін. Осы сынақтарда А оқиғасы m рет пайда болған болсын.
Сынақтарда А оқиғасының пайда болған санының осы тәжірибедегі барлық сынақтар санына қатынасын оқиғаның салыстырмалы жиілігі деп атайды және W(A) арқылы белгілейді. Сонда:
![]()
Мысал 2. Кітап дүкеніне түскен кітаптардың жетеуі сапасыз болып шықты. Сапасыз кітаптардың пайда болуының салыстырмалы жиілігі:
![]()
Сынақтар өскен сайын оқиғаның салыстырмалы жиілігі оқиғаның ықтималдығына жақындайды. Салыстырмалы жиіліктің осы қасиетін теңге лақтыру сынақтарының нәтижесінен байқауға болады:
|
Сынақтар саны |
Елтаңбаның пайда болу саны |
W(A) |
Сынақ жүргізуші |
|
4040 |
2048 |
0,5080 |
Ж. Бюффон |
|
12000 |
6019 |
0,5016 |
К. Пирсон |
|
24000 |
12012 |
0,5005 |
К. Пирсон |
Оқиғаның салыстырмалы жиілігі оқиғаның статистикалық анықтамасы деп аталады. Сонымен, ықтималдықтың классикалық анықтамасымен қатар статистикалық анықтамасы да қолданылады. Бұл жерде ескеретін жай, ол оқиғаның салыстырмалы жиілігі сынақтар өткізіліп болғаннан кейін есептелетіндігі және сынақтар саны мейлінше үлкен болғаны жөн.
3-сабақ. Комбинаторика формулалары
Мысал 1. Мерген нысанаға екi рет оқ атты. Аi-шi атқанда нысанаға тигiзуi (i=![]() ).
).
Ендi мына А - ең болмаса бiр рет тигiздi, В - бiр рет қана тигiздi, С - екi рет тигiздi, Д - екi рет тигiзе алмады оқиғаларын А1, А2 оқиғалары арқылы өрнекте.
Шешуi: А1,A2 - сәйкес бiрiншi және екiншi атқанда нысанаға тигiзуi, ал ![]() және
және ![]() - сәйкес бiрiншi, екiншi атқанында нысанаға тигiзе алмауы.
- сәйкес бiрiншi, екiншi атқанында нысанаға тигiзе алмауы.
Сонда А1+А2 оқиғасы, екi оқиғаның қосындысының анықтамасы бойынша не А1 не А2 немесе А1×А2 оқиғаларының пайда болатынын, яғни ең болмағанда бiр оқиғаның пайда болатынын көрсетедi, олай болса А=А1+А2.
Сол сияқты В= ![]() - тек бiр рет нысанаға тигiзу; С=
- тек бiр рет нысанаға тигiзу; С= ![]() - нысанаға екi рет тигiзу; D=
- нысанаға екi рет тигiзу; D= ![]() - екi рет тигiзбеуi.
- екi рет тигiзбеуi.
Мысал 2. Урнаға 4 ақ, 9 қара және 7 қызыл бiрдей шарлар салынған. Урнадан кез-келген бiр шар алынады. Сонда ақ шар пайда болуының ықтималдығы қандай?
Шешуi: А - ақ шар пайда болуы болсын.
Бұл тәжiрибеде элементарлық wi (i=![]() ) - оқиға дегенiмiз - урнадан кез-келген бiр шар алу. Шарлар бiрдей болғандықтан бұл wi оқиғалары тең мүмкiндi және өзара үйлесiмсiз. Элементарлық оқиғалардың жалпы саны осы урнадағы шарлар санына тең n=20, ал А оқиғасына қолайлы элементарлық оқиғалары саны урнадағы ақ шарлар санына тең. Сондықтан ықтималдықтың анықтамасы бойынша:
) - оқиға дегенiмiз - урнадан кез-келген бiр шар алу. Шарлар бiрдей болғандықтан бұл wi оқиғалары тең мүмкiндi және өзара үйлесiмсiз. Элементарлық оқиғалардың жалпы саны осы урнадағы шарлар санына тең n=20, ал А оқиғасына қолайлы элементарлық оқиғалары саны урнадағы ақ шарлар санына тең. Сондықтан ықтималдықтың анықтамасы бойынша:
![]()
Ықтималдық анықтамасын пайдаланып есептер шығарған кезде комбинаторика формулалары жиi қолданылады. Сондықтан, табиғаты әр түрлi болып келетiн, өзара айырмашылығы бар элементтерден құрастырылған комбинациялардың үш типiн қарастырайық.
Анықтама: Берiлген әртүрлi n элементтен m элемент бойынша орналастырулар деп, әрқайсысы бiр-бiрiнен не құрамы бойынша, не орналасу ретi бойынша ажыратылатын комбинацияларды айтады.
Орналастырулардың жалпы саны мына формуламен анықталады
![]() (1.1.7)
(1.1.7)
Анықтама: Берiлген әртүрлi n элементтен n элемент бойынша алмастырулар деп, әрқайсысы бiр-бiрiнен тек орналасу ретi бойынша ғана ажыратылатын комбинацияларды айтады.
Алмастырулардың жалпы саны:
![]() (1.1.8)
(1.1.8)
Сондай-ақ алмастыруларды орналастырулардың жеке түрi ретiнде қарастыруға болады, яғни
![]()
Анықтама: Берiлген әртүрлi n элементтен m элемент бойынша терулер деп, әрқайсысы бiр-бiрiнен тек құрамы бойынша ажыратылатын комбинацияларды айтады.
Терулердiң жалпы саны мына формуламен есептелiнедi:
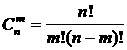 (1.1.9)
(1.1.9)
Бұл жерде n! (n факториaл) мына түрде есептелiнедi
n!=1×2×3×...×(n-1)×n және 0!=1 деп қабылданады.
Қосу ережесi: Егер әртүрлi А және В элементтердi сәйкес n және m рет жолмен таңдап ала алатын болсақ, онда осы екi элементтiң бiреуiн (А-ны болмаса В-ны) m+n рет жолмен таңдап алуға болады.
Көбейту ережесi: Егер бiр группада m элемент, ал екiншi группада n элемент болса, онда әрбiр группадан бiр элементтен алып құрылған қосақтардың саны n×m көбейтiндiсiне тең болады.
Расында бiрiншi группаның бiр элементi екiншi группаның әрбiр элементiмен қосақталынады және керiсiнше, сондықтан қосақтардың жалпы саны m×n көбейтiндiсiмен анықталады.
Мысал 1. Кiтап сөресiнде кездейсоқ ретпен 5 томнан тұратын анықтама қойылған:
а) Кiтаптар бiрiншi томнан бесiншi томға дейiн дұрыс ретпен орналасуының ықтималдығын табу керек.
в) Ең болмағанда бiр томның реттi орнында тұрмаған жағдайдың ықтималдығын табу керек.
Шешуi: Сынақ ретiнде кiтап сөресiнде кiтаптардың кез-келген ретпен қойылуын қарастырайық. Сонда кiтаптардың бұлай орналасуларының жалпы саны
n=P5=5!=120
1 А әрiпi арқылы кiтап сөресiнде кiтаптардың том нөмiрлерiнiң өсу ретiмен орналасуын бiлдiретiн оқиғаны белгiлейiк. Бұл оқиғаға қолайлы элементарлық оқиға бiреу-ақ. Сондықтан
P(A)= ![]() ;
;
2 В әрiпi арқылы, ең болмағанда бiр том реттi орнында болмауын бiлдiретiн оқиғаны белгiлейiк. Мұндай оқиғалар саны m=n-1, яғни m=119. Себебi кiтаптардың том нөмiрлерi бойынша дұрыс орналасу саны бiрге тең, ал қалған орналасулар В оқиғасын анықтайды. Сонымен P(B)=119/120;
Осы жерде А және В оқиғаларының қарама-қарсы екенiн ескерсек, онда ![]() екенiн пайдаланып
екенiн пайдаланып ![]() табамыз, яғни бұрынғы жауапты алдық.
табамыз, яғни бұрынғы жауапты алдық.
Мысал 2. Қорапта бiрдей 5 бұйым бар. Оның үшеуi боялған. Қораптан кезкелген екi бұйым алынды.
1 Алынған екi бұйымның бiреуi боялған бұйым болуының ықтималдығын табу керек.
2 Алынған бұйымның екеуi де боялған бұйым болуының ықтималдығын табу керек.
Шешуi: 1. Қорапта 5 бұйымның екеуiн барлығы ![]() тәсiлмен алуға болады, ал алынған екi бұйымның бiреуi боялған болса, сол бiр боялған, бiр боялмаған бұйымдарды сәйкес
тәсiлмен алуға болады, ал алынған екi бұйымның бiреуi боялған болса, сол бiр боялған, бiр боялмаған бұйымдарды сәйкес
![]()
![]() тәсiлмен алуға болады. Сонда екi бұйымның бiрi боялған болудың барлық қолайлы элементарлық оқиғалар саны
тәсiлмен алуға болады. Сонда екi бұйымның бiрi боялған болудың барлық қолайлы элементарлық оқиғалар саны
![]()
Сөйтiп ![]()
2. Алдыңғы пункттегi шығару жолын пайдаланып:
![]()
Сонда ![]()
Ықтималдықтарды есептегенде қайталанбалы алмастырулар, орналастырулар және терулер де пайдаланылады.
II-блок. Ықтималдықтарды көбейту және қосу теоремалары
4-сабақ. Ықтималдықтарды көбейту, қосу теоремалары және ең болмағанда бір оқиғаның пайда болуының ықтималдығы. қарама-қарсы оқиғалар
Ықтималдықтарды көбейту теоремасы:
Егер А және В тәуелдi оқиғалар болса, онда
![]() (1.2.1)
(1.2.1)
Егер А және В тәуелсіз оқиғалар болса, онда
![]() (1.2.2)
(1.2.2)
Егер А және В үйлесiмсiз оқиғалар болса, онда
![]() (1.2.3)
(1.2.3)
Егер А және В үйлесiмдi оқиғалар болса, онда
![]() (1.2.4)
(1.2.4)
A1, A2, A3, A4,..., An оқиғалары жинақ бойынша тәуелсiз болсын. Осы оқиғалардың ең болмағанда бiреуiнiң (А оқиғасы) пайда болуының ықтималдығы мына формуламен анықталады.
![]() (1.2.5)
(1.2.5)
Жеке жағдайда, егер A1, A2, A3,..., An оқиғаларының пайда болуының ықтималдықтары бiрдей болса, яғни
![]() ,
,
![]() (1.2.6)
(1.2.6)
 Мысал 1. 36 картаның iшiнен кезкелген 2 карта алынсын.
Осы екi картаның бiр түстi болуының ықтималдығын табу керек.
Мысал 1. 36 картаның iшiнен кезкелген 2 карта алынсын.
Осы екi картаның бiр түстi болуының ықтималдығын табу керек.
Шешуi: Әуелi алынған екi картаның белгiлi бiр түске жататынының (айталық "қарға" болсын) ықтималдығын табалық.
Белгiлеу енгiзелiк. А - бiрiншi карта "қарға" болсын, В - екiншi карта да "қарға" болсын.
Бұл екi оқиға тәуелдi оқиғалар, яғни В-ның пайда болу ықтималдығы А-ның пайда болуына, не пайда болмауына байланысты
өзгерiп отырады.
Сондықтан ![]() ,
, ![]()
Осыдан ![]()
Ал ендi A1, A2, A3, A4 алынған екi карта сәйкес төрт түстiң бiрiне жататындығын көрсететiн өзара үйлесiмсiз оқиғалар болсын. Сонда алынған екi картаның бiрдей түстi (оқиға С) болуы A1, A2, A3, A4 оқиғаларының кез-келгенi орындалса пайда болады, яғни C= A1 + A2 +A3 +A4 ;
Олай болса ![]()
Мысал 2. Екi мерген атыс алаңында атыс жүргiзуде. Бiрiншi мергеннiң нысанаға тигiзу ықтималдығы - 0,7, екiншiсiнiкi - 0,8 тең. Егер екеуi де бiр-бiрден атыс жасаса, ең болмағанда бiреуiнiң нысанаға дәл тигiзетiндiгiнiң ықтималдығы қандай?
Шешуi: Белгiлеу енгiзелiк. А - бiрiншi мерген нысанаға дәл тигiздi. В - екiншi мерген нысанаға дәл тигiздi. Бұл екi оқиға үйлесiмдi, себебi екi мерген де нысанаға дәл тигiзуi мүмкiн ғой. Сондықтан үйлесiмдi оқиғалардың қосындыларының ықтималдығы туралы теореманы (1.2.4) пайдаланып:
![]() екенiн табамыз.
екенiн табамыз.
Осы мысалды ең болмағанда бiр оқиғаның пайда болуы (оқиға D) туралы теореманы пайдаланып та шығаруға болатынын көрсетелiк. Шынында да D - оқиғасы ең болмаса бiреуiнiң нысанаға тигiзуi болсын. Сонда
![]()
Бұл жерде ![]()
![]()
Мысал 3. Екi жәшiкке детальдар салынған. Бiрiншi жәшiкте 10 деталь, оның үшеуi стандартты, екiншiсiнде - 15 деталь, онда 6 стандартты бар. Әрбiр жәшiктен бiр-бiрден кез-келген деталь алынды. Алынған екi детальдiңде стандартты екенiнiң ықтималдығын табу керек.
Шешуi: Белгiлеу енгiзелiк. А - бiрiншi жәшiктен алынған деталь стандартты, В - екiншi жәшiктен алынған деталь стандартты. Сондықтан ![]() . Алынған екi детальде стандартты болуы үшiн А×В оқиғасы пайда болуы керек. Бұл екi оқиғада үйлесiмдi, себебi екеуi бiрдей пайда бола алады, сондай-ақ бұл оқиғалар тәуелсiз, себебi олардың пайда болуы бiр-бiрiне байланыссыз. Сондықтан /1.2.2./ формуланы пайдалануға болады:
. Алынған екi детальде стандартты болуы үшiн А×В оқиғасы пайда болуы керек. Бұл екi оқиғада үйлесiмдi, себебi екеуi бiрдей пайда бола алады, сондай-ақ бұл оқиғалар тәуелсiз, себебi олардың пайда болуы бiр-бiрiне байланыссыз. Сондықтан /1.2.2./ формуланы пайдалануға болады:
![]()
Мысал 4. Деталь дайындау процессi үш операциядан тұрады. Бiрiншi операция кезiнде сапасыз деталь дайындалудың ықтималдығы - 0,02, ал екiншi операция кезiнде - 0,03 және үшiншi операция кезiнде - 0,07. Сапасыз детальдердiң пайда болуын тәуелсiз оқиғалар деп қарастырып, осы үш операциядан кейiн сапалы деталь дайындауының ықтималдығын табу керек.
Шешуi: Белгiлеу енгiзелiк. А оқиғасы деп бiрiншi операциядан кейiн сапасыз детальдiң пайда болуы; В - екiншi операциядан кейiн сапасыз деталь пайда болуы; С - үшiншi операциядан кейiн сапасыз деталь пайда болуы. Есептiң шарты бойынша А,В,С тәуелсiз оқиғалар. Олай болса ![]() оқиғалары да тәуелсiз оқиғалар. Сондықтан D=
оқиғалары да тәуелсiз оқиғалар. Сондықтан D= ![]() оқиғасы - үш операциядан кейiн сапалы деталь дайындалуын анықтайды. Ендi тәуелсiз оқиғалардың көбейтiндiсiнiң ықтималдығының формуласын
оқиғасы - үш операциядан кейiн сапалы деталь дайындалуын анықтайды. Ендi тәуелсiз оқиғалардың көбейтiндiсiнiң ықтималдығының формуласын
![]() пайдаланып табамыз.
пайдаланып табамыз.
Мысал 5. Сүңгуiр қайықты iздеп табудың ықтималдығы 0,8, ал оны жойып жiберудiң ықтималдығы 0,6 - ға тең. Iздеп табылған сүңгуiр қайықты жойып жiберудiң ықтималдығы қандай?
Шешуi: А - оқиғасы сүңгуiр қайықты iздеп тауып алуды бiлдiредi. В - сүңгуiр қайықты жойып жiберудi бiлдiредi. Сонда Р(А)=0,8; P(B)=0,6. Есептiң шарты бойынша iздеп табылған қайықты жойып жiберудiң ықтималдығын табу керек, яғни РA(B) ықтималдығын табу керек.
P(B)=P(A) ×PA(B)
Сонда ![]()
Мысал 6. Үш баскетболшы корзинаға бiр-бiрден доп лақтырды. Бiрiншi баскетболшының корзинаға доп түсiруiнiң ықтималдығы 0,9, екiншiсiнiкi - 0,8, үшiншiсiнiкi - 0,7. Тек бiр баскетболшының корзинаға доп түсiруiнiң ықтималдығы қандай?
Шешуi: А - бiрiншi баскетболшының корзинаға доп түсiруi, В,С - екiншi, үшiншi баскетболшының корзинаға доп түсiруi. Бұл оқиғалар тәуелсiз. Ендi мына оқиғаларды қарастырайық: ![]() -тек А оқиғасының пайда болуы,
-тек А оқиғасының пайда болуы, ![]() - тек В оқиғасының пайда болуы,
- тек В оқиғасының пайда болуы, ![]() - тек С оқиғасының пайда болуы.
- тек С оқиғасының пайда болуы.
Бұл соңғы үш оқиғалар үйлесiмсiз сондықтан
![]()
оқиғасы А,В,С оқиғаларының тек бiреуiнiң пайда болуын бiлдiредi. Сөйтiп
![]()
Мысал 7. Үш аңшы үшып бара жатқан үйректi сәйкес 2/3, 3/4, 1/4 ықтималдықтарымен атып түсiре алады. Ұшып бара жатқан үйректi үшеуi де бiр мезгiлде атты. Үйректi атып түсiргендiктiң ықтималдығы қандай?
Шешуi: Үйрек атып түсiру үшiн ең болмағанда бiр аңшының оғы дәл тиюi керек. Сондықтан
![]() (1.2.5) формуланы пайдаланып табамыз.
(1.2.5) формуланы пайдаланып табамыз.
Мұндағы А – үйрек атып түсiрiлдi, А1- үйректi бiрiншi аңшы атып түсiрдi; А2- үйректi екiншi аңшы атып түсiрдi; А3- үйректi үшiншi аңшы атып түсiрдi.
5-сабақ. Толық ықтималдық. Бейес формуласы
Егер А оқиғасы, өзара үйлесiмсiз, толық группа құратын В1, В2,...,Вn оқиғаларының (гипотезаларының) бiреуiмен бiрге пайда болатын болса, онда А оқиғасының ықтималдығы мына формуламен анықталады:
![]() (1.3.1)
(1.3.1)
Мұндағы ![]() - шартты ықтималдықтар. Бұл (1.3.1) формула толық ықтималдықтың формуласы деп аталады.
- шартты ықтималдықтар. Бұл (1.3.1) формула толық ықтималдықтың формуласы деп аталады.
Сондай-ақ жоғарыдағы шарттар сақталғанда Бейес формуласы орындалады:
![]() (1.3.2)
(1.3.2)

Бұл (1.3.2) формула гипотезалардың ықтималдығын А оқиғасы пайда болғаннан кейiн есептеуге қолданылады.
Мысал 1. Қоймаға үш партия радиошамдар әкелiндi. Алынған кез-келген радиошамның осы партиялардың әрқайсысынан алынуының сәйкес ықтималдықтары 0,25; 0,5; 0,25 тең. Ал әрбiр партиядағы радиошамдардың белгiлi мерзiм жұмыс iстеп шығуларының ықтималдықтары сәйкес 0,7; 0,6; 0,8.
1. Осы партиялардың бiрiнен алынған радиошамның белгiлi мерзiм жұмыс iстеп шығуының ықтималдығы қандай?
2. Мерзiмдi уақыт жұмыс iстеп шыққан радиошамның екiншi партиядан алынғандығының ықтималдығын табу керек.
Шешуi: 1. Бұл мысалды шығару үшiн толық ықтималдықтың формуласын және Бейес формуласын қолдану қажет. Ол үшiн әуелi қарастырып отырған оқиғаларды белгiлеп алайық:
А - радиошам белгiлi мерзiм жұмыс iстейдi;
В1 - радиошам бiрiншi партиядан алынған;
В2 - радиошам екiншi партиядан алынған;
В3 - радиошам үшiншi партиядан алынған.
Сонда P(B1)=0,25 ![]()
P(B2)=0,5 ![]()
P(B3)=0,25 ![]()
В1, В2, В3 оқиғалар үйлесiмсiз және толық группа құрайды. Толық группа құрайтындығын тексерейiк.
P(В1 +В2 +В3)= P(В1)+P(В2)+P(В3)=0,25+0,5+0,25=1
Сонымен толық ықтималдық формуласының шарттары орындалады, олай болса
P(A)= 0,25×0,7+0,5×0,6+0,25×0,8=0,675
2. Ендi мерзiмдi уақыт жұмыс iстеп шыққан радиошамның екiншi партиядан алынғандығының ықтималдығын Бейес формуласын пайдаланып табамыз.
PA(B2)=0,5×0,6/0,675=0,445
Сол сияқты PA(B3), PA(B1) табалық
PA(B1)=175/675, PA(B3)=200/675
Бұл жерде PA(B1)+ PA(B2)+ PA(B3)=1 екенiн ескертемiз.
Байқап отырғанымыздай, А оқиғасы пайда болғаннан кейiн есептелiнген мына PA(Bi) (i=1, 2, 3) шартты ықтималдықтар В1, B2, B3 гипотезаларының ықтималдықтарының өзгергенiн көрсетедi.
Ескерту ретiнде айтарымыз, бұл (1.3.1) және (1.3.2) формулаларды қолданғанда алынған В1, B2, ..., Bn гипотезаларының үйлесiмсiздiгiн және толық группа құратындығын тексеру қажет.
Мысал 2. 350 механизмдердiң 160 - бiрiншi сортқа, 110 екiншi сортқа, 80 - үшiншi сортқа жатады. Бiрiншi сортқа жататын механизмдердiң iшiнде сапасыз механизм болуының ықтималдығы 0,01, екiншi сортқа жататындардың арасында - 0,02, үшiншi сортқа жататындардың арасында - 0,04 тең. Кез-келген бiр механизм алынған. Алынған механизмнiң сапалы екенiнiң ықтималдығын табу керек.
Шешуi: Белгiлеу енгiзелiк:
А - алынған механизм сапалы;
В1 - алынған механизм бiрiншi сортқа жатады;
В2 - алынған механизм екiншi сортқа жатады;
В3 - алынған механизм үшiншi сортқа жатады;
Сонда
P(B1)=160/350 ![]()
P(B2)=110/350 ![]()
P(B3)=80/350 ![]()
В1, B2, B3 оқиғалары үйлесiмсiз. Расында, айталық B3 оқиғасы пайда болды делiк, яғни алынған бiр механизм үшiншi сортқа жатады, олай болса В1, B2 оқиғасы B3 оқиғасымен бiрге пайда бола алмайды деген сөз. Себебi алынған бiр механизм бiр уақытта әрi үшiншi, әрi екiншi, әрi бiрiншi сортқа жатуы мүмкiн емес қой.
Сондай- ақ В1, B2, B3 оқиғалары толық группа құрайды
![]()
Олай болса (1.3.1.) формуласын қолданып,
![]()
Мысал 3. Бiрдей үш жәшiкке бiрдей өлшемдi шарлар салынған. Бiрiншi жәшiкте 10 ақ, 5 қара, 3 қызыл, екiншi жәшiкте 9 ақ, 16 қара, 11 қызыл, үшiншi жәшiкте 7 ақ, 4 қара, 1 қызыл шарлар бар. Кез-келген жәшiктен кез-келген шар алынды. Алынған шардың қара шар болуының ықтималдығы қандай?
Шешуi: Мына оқиғаларды қарастырайық:
А - алынған шардың түсi қара;
В1- шар бiрiншi жәшiктен алынды;
В2- шар екiншi жәшiктен алынды;
В3- шар үшiншi жәшiктен алынды.
Қарастырып отырған В1, B2, B3 оқиғалары үйлесiмсiз. Расында, егер, айталық, шар екiншi жәшiктен алынса, онда B2 оқиғасы пайда болады да, В1, B3 оқиғалары пайда бола алмайды. Ойымызды осылай жалғастырып В1, B2, B3 оқиғаларының үйлесiмсiз екенiне көз жеткiзуге болады. Ал А оқиғасы В1, B2, B3 оқиғаларына тәуелдi. Ендi үш жәшiктiң бiрдей екенiн ескерiп:
; P(B1)=1/3, ![]()
; P(B2)=1/3 ![]()
; P(B3)=1/3 ![]()
Осыдан ![]() .
.
Мысал 4. Бiрiншi урнаға 1 ақ, 3 қара, ал екiншi урнаға 4 ақ, 6 қара бiрдей шарлар салынған. Бiрiншi урнадан бiр шар алынып екiншi урнаға салынды. Содан кейiн екiншi урнадан шар алынды. Екiншi урнадан алынған шардың түсi қара болуының ықтималдығы қандай?
Шешуi: Мына оқиғаларды қарастырайық. В1 - бiрiншi урнадан ақ шар алынды. В2- бiрiншi урнадан қара шар алынды, А - екiншi урнадан қара шар алынды.
Бұл жерде В1, В2 оқиғаларын қарастыру себебi, ол әуелi бiрiншi урнадан қандай тұстi шар алуға байланысты. Бұл екi оқиғаға үйлесiмсiз және толық группа құрайды. Ендi
P(B1)=3/4 ![]()
; P(B2)=1/4 ![]()
Сонда толық ықтималдықтың формуласы бойынша
![]()
Ендi осы есептiң шарты орындалсын. Сонда екiншi урнадан алынған қара шар бастапқыда бiрiншi урнадан алынғандығының ықтималдығын табайық:
![]()
III-блок. Тәуелсіз сынақтар
6-сабақ. Якоб Бернулли
Нәтижелерiнде тәуелсiз оқиғалар пайда болатын сынақтарды тәуелсiз сынақтар деп атайды. Екi ғана нәтижесi бар тәуелсiз сынақтарды қарастыралық. Мұндай сынақтарға теңге лақтыру, бұйымның сапалылығын тексеру, детальдiң жарамдылығын тексеру т.б. сынақтар жатады.
Сонымен аталған екi нәтиженi "А оқиғасы пайда болады" және "А оқиғасы пайда болмайды" деп атаймыз, сондай-ақ осы екi оқиғаның бiр-бiрiне қарама-қарсы екенiн ескерiп, сәйкес ықтималдықтарын P(A)=p және ![]() деп аламыз, яғни А оқиғасының ықтималдығы тұрақты. Осындай шарттар орындалғанда Бернулли схемасы орынды деп айтады.
деп аламыз, яғни А оқиғасының ықтималдығы тұрақты. Осындай шарттар орындалғанда Бернулли схемасы орынды деп айтады.
Тәуелсiз n сынақтарда ықтималдығы тұрақты болатын А оқиғасының дәл к рет пайда болуының ықтималдығы Бернулли формуласымен есептеледi:
![]() (1.4.1)
(1.4.1)
Мұндағы p=P(A), q=1-p= ![]() . Бұл формуланы кейде биномдық деп те атайды.
. Бұл формуланы кейде биномдық деп те атайды.
Бернулли формуласын пайдаланып мына оқиғалардың ықтималдығын анықтауға болады:
1. Тәуелсiз n сынақтарда А оқиғасының к реттен кем пайда болатындығының ықтималдығы:
![]() (1.4.3)
(1.4.3)
2. к реттен артық болуының ықтималдығы:
![]() (1.4.4)
(1.4.4)
3. Кем дегенде к рет пайда болуының ықтималдығы:
![]() (1.4.5)
(1.4.5)
4. к реттен артық емес пайда болуының ықтималдығы
![]() (1.4.6)
(1.4.6)
Бернулли схемасында сынақтар тәуелсiз болғандықтан, осы сынақтарда ең болмаса бiр оқиғаның пайда болуының ықтималдығы мына формуламен анықталады:
P=1-qn (1.4.7)
Мысал 1. Шахмат ойнау шеберлiгi тең екi шахматшы ойын көрсетуде. Тең аяқтаған ойынды есептемегенде:
1 Төрт партияның үшеуiн ұту мен сегiз партияның бесеуiн ұтудың ықтималдықтарын табу керек. Қайсысының ықтималдығы жоғары?
2 Төрт партиядан кем дегенде үш партия ұту мен сегiз партиядан кем дегенде 5 партия ұтудың ықтималдықтарын табу керек. Қайсысының ықтималдықтары жоғары?
Шешуi: Ойнау шеберлiгi тең болғандықтан олардың әрбiр партияда ұту ықтималдықтары 0,5 тең.
1. Төрт партиядан үш ұтыстың ықтималдығы Бернулли формуласы (1.4.1) бойынша
![]()
Сегiз партияда 5 ұтыстың ықтималдығы
![]()
Осыдан ![]() , яғни төрт партиядан үш ұтыстың ықтималдығы, сегiз партиядан 5 ұтыстың ықтималдығынан жоғары.
, яғни төрт партиядан үш ұтыстың ықтималдығы, сегiз партиядан 5 ұтыстың ықтималдығынан жоғары.
2. Төрт партиядан кем дегенде үш ұтыстың ықтималдығы
![]()
Сегiз партиядан кем дегенде 5 партия ұтудың ықтималдығы
![]()
Осыдан 93/256 > 5/16, яғни сегiз партиядан кем дегенде бес ұтыстың ықтималдығы, төрт партиядан кем дегенде 3 партия ұтыстың ықтималдығынан жоғары.
Ескерту: Егер Бернулли схемасында сынақтар саны үлкен болса, онда Бернулли формуласын пайдалану үлкен арифметикалық есептеулерге келтiредi. Сондықтан бұл жағдайда жуықтап есептеу формулаларын қолданады.
Егерде P(A)=p мәнi 0,5-тiң маңайында болса, онда Муавр-Лапластың локалдық және интегралдық жуықтау формулалары қолданылады.
7-сабақ. Муавр- Лапластың төңіректік (локальды) және интегральды теоремалары
Тәуелсiз n сынақтарда ықтималдығы тұрақты А оқиғасының тура к рет пайда болуының ықтималдығы мына формула бойынша жуықтап есептеледi:
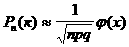 ,
,
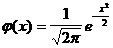 ,
,
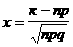 (1.4.8)
(1.4.8)
Муавр-Лапластың интегралды теоремасы:
Тәуелсiз n сынақтарда ықтималдығы тұрақты А оқиғасының к1- ден кем емес к2- ден артық емес рет пайда болуының ықтималдығы мына формула бойынша жуықтап есептеледi:
![]()
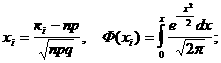 (1.4.9)
(1.4.9)
Мұндағы j(х), Ф(хi) функцияларының мәндерiнiң кестесi бөлек келтiрiлген.
8-сабақ. Ең ықтималды сан. Тәуелсіз сынақтарда оқиғаның салыстырмалы жиілігінің оқиғаның ықтималдығынан ауытқуы
А оқиғасының ең ықтималды m0 рет пайда болуы мына теңсiздiктен анықталады:
![]() (1.4.2)
(1.4.2)
Егер np-q- бүтiн сан болса, онда m0-дiң екi бүтiн мәнi болады, ал np-q- бүтiн сан болмаса, онда m0- дiң бiр ғана бүтiн мәнi болады.
Муавр-Лапластың (1.4.9) формуласын пайдаланып тәуелсiз сынақтарда А оқиғасының ықтималдығының салыстырмалы жиiлiктен ауытқуының абсолют шамасының ықтималдығы мына формула арқылы табылады:
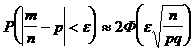 (1.4.10)
(1.4.10)
Егерде P(A)=p мәнi 0,5 -тен едәуiр кiшi болса онда басқа жуықтау формуласы - Пуассон формуласы қолданылады:
![]() , l=np (1.4.11)
, l=np (1.4.11)
Жаттығу есептері
1. Жәшiктегi 15 детальдiң 10-ны боялған. Жинаушы кез келген 3 деталь алды. Алынған 3 деталь де боялғандығының ықтималдығы қандай?
2. Бiрiншi жәшiкте нөмiрлерi 1- ден 5 - ке дейiн, ал екiншiсiнде 6-дан 10-ға дейiн шарлар бар. Әрбiр жәшiктен бiр-бiрден шар алынды. Алынған екi шардың нөмiрлерiнiң қосындысы 11 болуының ықтималдығы қандай?
3. Жәшiктегi 10 детальдiң 4-i боялған. Деталь жинаушы 3 деталь алды. Алынған үш детальдiң ең болмағанда бiреуi боялғандығының ықтималдығын табу керек.
4. Ақшалай-заттай лотереяда әрбiр 10000 билетке 150 заттай және 50 ақшалай ұтыс шығады. Бiр билетi бар адамға не заттай, не ақшалай ұтыс шығуының ықтималдығы қандай?
5. Урнада 10 қызыл, 5 көк және 15 ақ шарлар бар. Түстi шардың алынуының ықтималдығы қандай?
6. Екi жәшiкте 20 детальден бар. Оның iшiнде бiрiншi жәшiкте 17 стандартты, екiншi жәшiкте 15 стандартты деталь бар. Екiншi жәшiктен кез-келген бiр деталь алынып бiрiншi жәшiкке салынған. Содан кейiн бiрiншi жәшiктен кез-келген бiр деталь алынды. Бiрiншi жәшiктен алынған детальдiң стандартты болуының ықтималдығын табу керек.
7. Гаражда 5 машина бар. Кез-келген бiр сәтте машиналардың жұмыс iстеу ықтималдығы 0,8-ге тең. Қалаған бiр сәтте үш машинаның жұмыс iстеуiнiң ықтималдығы қандай?
8. Цехтағы 6 мотордың әрқайсысының белгiлi бiр сәтте iстеп тұрғандығының ықтималдығы 0,8-ге тең.
9. Белгiлi бiр сәтте 4 мотордың iстеп тұруының ықтималдығын табу керек.
 II-ші Модуль. Кездейсоқ шамалар:
II-ші Модуль. Кездейсоқ шамалар: II МОДУЛЬ
КЕЗДЕЙСОҚ ШАМАЛАР
I-блок. Дискретті кездейсоқ шамалар
9-сабақ. Дискретті кездейсоқ шамалардың үлестірім заңы
Айталық элементарлық оқиғалар кеңiстiгi ![]() берiлсiн. Егер осы кеңiстiкте анықталған Х(w) функциясы сандық мәндер қабылдап, кез-келген x үшiн мына ықтималдық
берiлсiн. Егер осы кеңiстiкте анықталған Х(w) функциясы сандық мәндер қабылдап, кез-келген x үшiн мына ықтималдық
P(X<x)=P{w: X(w)<x}
анықталған болса, онда X{w} функциясын кездейсоқ шама деп атайды.
Кездейсоқ шамалар мен кездейсоқ оқиғаларды бiр-бiрiнен ажырата бiлген жөн. Анықтамадан байқап отырғанымыздай кездейсоқ шама мiндеттi түрде пайда болады, тек оның қандай мәндi қабылдайтыны алдын-ала белгiсiз. Ал кездейсоқ оқиғаның пайда болуының өзi кездейсоқ жай.
Мысалы, теңге лақтыру тәжiрибесiн қарастырайық. Осы тәжiрибеде кездейсоқ оқиға деп елтаңбаның немесе цифрдiң пайда болуын айтамыз, ал кездейсоқ шама ретiнде тәжiрибе нәтижесiнде елтаңбаның пайда болу санын қарастыруға болады. Бұл кездейсоқ шаманың мүмкiн мәндерi 0, 1, 2 ...,n, яғни тәжiрибе нәтижесiнде елтаңба мүлде пайда болмауы мүмкiн, немесе 1 рет, 2 рет, ..., n рет пайда болуы мүмкiн. Кездейсоқ шамалар дискреттi және үзiлiссiз болып бөлiнедi.
Кездейсоқ шамалардың кейбiр мысалдарын келтiрелiк:
1. Тәуелсiз n сынақтарда тұрақты ықтималдықпен А оқиғасының пайда болу саны;
2. Бiр цех өнiмдерiнiң iшiндегi сапасыз бұйымдар саны;
3. Снарядтың үшу алыстығы;
4. Телефон станциясына белгiлi бiр уақыт мерзiмiнде келiп түскен тапсырыстар саны, т.б.
Осы мысалдардан көрiп отырғанымыздай кездейсоқ шама тәжiрибенiң кездейсоқ нәтижесiнiң сандық сипаттамасы екенiн байқаймыз.
Анықтама. Кездейсоқ шаманың қабылдайтын мәндерiнiң саны ақырлы болса немесе тiзбек түрiнде жазылса, онда ондай кездейсоқ шамаларды дискреттi кездейсоқ шамалар деп атайды.
Дискреттi кездейсоқ шаманы анықтау үшiн үлестiрiм қатары - үлестiрiм кестесi құрылады.
|
Х |
x1 |
x2 |
x3 |
... |
xn |
|
p |
p1 |
p2 |
p3 |
... |
pn |
Кестенiң жоғары жолында кездейсоқ шаманың мүмкiн мәндерi, ал төменгi жолында - сол мәндердiң сәйкес ықтималдықтары келтiрiлген.
Мұнда ![]() .
.
9.1 БИНОМДЫҚ ҮЛЕСТIРIМ
Егер мүмкiн мәндерi 0,1,2,..., к , ... болып, ал осы мүмкiн мәндердi қабылдау Х=к ықтималдықтары Бернулли формуласымен анықталса
![]() (2.1.1)
(2.1.1)

онда кездейсоқ шама биномдық үлестiрiм заңымен берiлген деп аталады.
Сонымен биномдық үлестiрiм заңдылығымен берiлген дискреттi кездейсоқ шаманы - тұрақты ықтималдықты А оқиғасының n тәуелсiз сынақтарда пайда болуының саны ретiнде қарастыруға болады.
9.2 Пуассон үлестірімі

Егер тәуелсiз сынақтарда n үлкен сан болса және р-ның шамасы аз болса, онда кездейсоқ шаманың мүмкiн мәндерiнiң сәйкес ықтималдықтарын Пуассон формуласымен
P(X=x)=Pn(к)» ![]() , l=np (2.1.2)
, l=np (2.1.2)
есептеу керек.
Бұл жағдайда кездейсоқ шама Пуассондық үлестiрiм заңымен берiлген дейдi. Бернулли схемасына негiзделген тағыда басқа үлестiрiмдердi келтiрелiк.
9.3 ГЕОМЕТРИЯЛЫҚ ҮЛЕСТIРIМ
Айталық тәуелсiз сынақтарда Бернулли схемасы қарастырылсын, мұнда P(A)=p. Сонда қатарынан (к-1) рет ![]() оқиғасы пайда болып, ал к -шы ретте А оқиғасының пайда болу ықтималдығы мына формуламен анықталады
оқиғасы пайда болып, ал к -шы ретте А оқиғасының пайда болу ықтималдығы мына формуламен анықталады
Г(к,р)=(1-р)к-1рm (2.1.3)
Ықтималдығы осы формуламен анықталған (к=1,2,3...,n) кездейсоқ шаманы геометриялық үлестiрiмiмен берiлген дейдi.
9.4 Блез Паскаль
Тәуелсiз сынақтарда ![]() оқиғасы қатарынан к-1 рет пайда болып, сосын А оқиғасы m рет пайда болуының ықтималдығы мына формуламен анықталады.
оқиғасы қатарынан к-1 рет пайда болып, сосын А оқиғасы m рет пайда болуының ықтималдығы мына формуламен анықталады.
![]() (2.1.4)
(2.1.4)
Ықтималдығы осы формуламен анықталған кездейсоқ шама Паскаль үлестiрiмiмен берiлген дейдi. Геометриялық үлестiрiм Паскаль үлестiрiмiнiң жеке жағдайы, яғни m=1 болғанда геометриялық үлестiрiмдi аламыз.
9.5 ГИПЕРГЕОМЕТРИЯЛЫҚ ҮЛЕСТIРIМ
Егер X кездейсоқ шамасының мүмкiн мәндерi 0,1,2,3 ...к болып, ал сәйкес ықтималдықтары мына формуламен
![]() (2.1.5)
(2.1.5)
анықталса, онда кездейсоқ шама гипергеометриялық үлестiрiммен берiлген дейдi.
Мысал 1. Жәшiкте барлығы 10 шар бар, олардың 7 - i қара 3-i көк шарлар. Жәшiктен кез-келген 5 шар алынды. Сол 5 шардың үшеуi қара болуының ықтималдығы қандай?
Шешуi: Осындай мазмұнды есептi классикалық анықтаманы және комбинаторикадағы қосу және көбейту ережелерiн пайдаланып шығаруға болады. Бұл есептi солай шығарса ![]()
![]() болады.
болады.
Ендi осы есептi жалпы түрде келтiрейiк.
Мысал 2. Жәшiкте барлығы N шарлар бар, оның iшiнде n қара шар бар, ал (N-n) - көк шарлар. Жәшiктен кез-келген m шар алынды. Сол алынған m шардың iшiнде к қара шар болуының ықтималдығы қандай?
Шешуi: x - жәшiктен алынған шарлар саны. Бұл кездейсоқ шаманың мүмкiн мәндерi 0, 1, 2, ..., m.
Жәшiктегi N шардан m шарды әртүрлi ![]() жолмен алуға болады, ал n қара шарлардан к шарды әртүрлi
жолмен алуға болады, ал n қара шарлардан к шарды әртүрлi ![]() жолмен алуға болады, сонда алынған m шардың iшiнде m-к көк шарлар болғандықтан барлық N-n көк шарлардан m - к көк шарды
жолмен алуға болады, сонда алынған m шардың iшiнде m-к көк шарлар болғандықтан барлық N-n көк шарлардан m - к көк шарды ![]() жолмен алуға болады. Сонымен жәшiктен алынған шардың к қара шарын
жолмен алуға болады. Сонымен жәшiктен алынған шардың к қара шарын ![]() жолмен, ал қалған m-к көк шарды
жолмен, ал қалған m-к көк шарды ![]() жолмен алуға болады екен. Олай болса комбинаторикадағы көбейту ережесiн қолдансақ, алынған m шардың iшiнде к - қара шар, m-к - көк шар болуы
жолмен алуға болады екен. Олай болса комбинаторикадағы көбейту ережесiн қолдансақ, алынған m шардың iшiнде к - қара шар, m-к - көк шар болуы ![]() ×
× ![]() жолмен анықталады.
жолмен анықталады.
Сонда ықтималдықтың классикалық анықтамасы бойынша
![]()
болады.
Сөйтiп X-кездейсоқ шама гипергеометриялық үлестiрiммен берiлгенiне көз жеткiздiк.
Мысал 3. Теңге үш рет лақтырылсын. Кездейсоқ шама Х ретiнде елтаңбаның пайда болу санын қарастырамыз.
1. Үлестiрiм қатарын жазу керек.
2. Үлестiрiм көпбұрышын салу керек.
3. M(x) , D(x) , s(х)-тарды табу керек.
Шешуi : Бұл кездейсоқ шама Х - тiң мүмкiн мәндерi 0, 1, 2, 3. Себебi теңгенi үш рет лақтырғанда елтаңба не пайда болмауы мүмкiн, не бiр рет пайда болуы мүмкiн т.с.с. Ал әрбiр лақтырғанда елтаңбаның пайда болу ықтималдығы 0,5 - ке тең. Олай дейтiнiмiз теңге лақтырғанда негiзiнен не елтаңба, не цифр пайда болады, ал теңгенiң симметриялығын ескерсек бұл екеуiнiң пайда болу ықтималдығы тең. Сондықтан бұл кездейсоқ шама Х- тi биномдық үлестiрiм заңымен сипаттауға болады.
Үлестiрiм қатарын жазайық:
|
Х |
0 |
1 |
2 |
3 |
|
Р |
|
|
|
|
немесе
|
Х |
0 |
1 |
2 |
3 |
|
Р |
1/8 |
3/8 |
3/8 |
1/8 |
Бұл жерде ![]() орындалады.
орындалады.
2. Үлестiрiм көпбұрышын салайық
.gif)
3. Математикалық үмiттi (2.1.6) формуламен есептеймiз :
![]()
Ал дисперсияны әдетте жеңiлдетiлген (2.1.8) формуламен есептейдi. Ол үшiн х2 кездейсоқ шаманың үлестiрiм қатарын жазып алу керек.
|
Х2 |
0 |
1 |
4 |
9 |
|
р |
1/8 |
3/8 |
3/8 |
1/8 |
Сонда
.gif)
Сондай-ақ бұл мысалдағы кездейсоқ шаманың биномдық үлестiрiммен берiлгенiн ескерсек, онда сандық сипаттамаларды (2.1.12) формулаларын пайдаланып та есептеуге болады :
![]()
Мысал 4. Берiлген партияның 10 процентi сапасыз бұйымдар. Кез-келген 4 бұйым алынды. Осы төрт бұйымдардың iшiнде сапасыз бұйымдардың пайда болу санының үлестiрiм заңын жазу керек. Сандық сипаттамаларын есептеу керек.
Шешуi : Х- сапасыз бұйымдардың пайда болуының саны. Әрбiр сапасыз бұйымның пайда болу ықтималдығы 0,1-ге тең, себебi берiлген партияның 10 процентi сапасыз бұйымдар. Бұл кездейсоқ шама биномдық үлестiрiм заңымен берiлген. Мұнда
n =4, p = 0,1 , q = 0,9.
Сонда
|
Х |
0 |
1 |
2 |
3 |
4 |
|
Р |
|
|
|
|
|
немесе
|
Х |
0 |
1 |
2 |
3 |
4 |
|
Р |
0,6581 |
0,2916 |
0,0486 |
0,0036 |
0,0001 |
Ендi математикалық сипаттамаларын табайық
М(X) = 4×0,1=0,4 , D(X) = 4×0,1×0,9= 0,36 , s(X) = 0,6.
Мысал 5. Айталық 12 бұйымның 8-i бiрiншi сортқа жатады. Кез келген 5 бұйым алынды. Сонда осы 5 бұйымның iшiнде бiрiншi сортты бұйымдардың болуының үлестiрiм кестесiн құрыңыз.
Шешуi : Есептiң шарты бойынша N=12 , m=5 , n=8. Кездейсоқ шама Х. Оның мүмкiн мәндерi : 1, 2, 3, 4, 5. Мұнда мүмкiн мәндер бiрден басталуының себебi : 5 бұйымның iшiнде кем дегенде бiр бұйым бiрiншi сортқа жатады.
Сонда
![]()
Ендi үлестiрiм кестесiн жазалық
|
Х |
1 |
2 |
3 |
4 |
5 |
|
Р |
0,0101 |
0,1414 |
0,4242 |
0,3535 |
0,0707 |
10-сабақ. Дискретті кездейсоқ шамалардың сандық сипаттамалары
Дискреттi кездейсоқ шаманың математикалық үмiтi деп оның мүмкiн мәндерiнiң сәйкес ықтималдықтарына көбейтiндiлерiнiң қосындысын айтады:
.gif) (2.1.6)
(2.1.6)
Дискреттi кездейсоқ шаманың дисперсиясы деп, оның өзiнiң математикалық үмiтiнен ауытқуының квадратының математикалық үмiтiн айтады:
.gif) (2.1.7)
(2.1.7)
Дисперсияны есептеудiң жеңiлдетiлген формуласы :
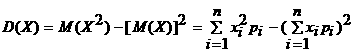 (2.1.8)
(2.1.8)
Дискреттi кездейсоқ шаманың орташа квадраттық ауытқуы мына формуламен есептелiнедi:
![]()
Дискреттi кездейсоқ шаманың бастапқы к - реттi моментi деп осы кездейсоқ шаманың к-шы дәрежесiнiң математикалық үмiтiн айтады:
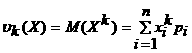 (2.1.9)
(2.1.9)
Дискреттi кездейсоқ шаманың к - реттi орталық моментi деп, оның өзiнiң математикалық үмiтiнен ауытқуының к-шы дәрежесiнiң математикалық үмiтiн айтады :
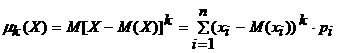 (2.1.10)
(2.1.10)
Кездейсоқ шаманың математикалық үмiтi бiрiншi бастапқы моментiне, ал дисперсиясы - екiншi орталық моментiне тең :
![]() ,
, ![]()
Сондай-ақ екiншi, үшiншi және төртiншi орталық моменттер
бастапқы моменттер арқылы төмендегiдей өрнектеледi :
![]() ,
, ![]() ,
,
![]() (2.1.11)
(2.1.11)
Дискреттi кездейсоқ шаманың ең ықтималды мәнiн оның Модасы (M0) деп атайды.
Айталық кездейсоқ шаманың n мүмкiн мәндерi болсын.
![]()
теңдiгi орындалса, онда ![]() кездейсоқ шаманың медианасы деп аталады.
кездейсоқ шаманың медианасы деп аталады.
Егер n=2к болса, онда ![]() , егерде n=2к+1 болса, онда
, егерде n=2к+1 болса, онда ![]()
Сондай-ақ қарастырылып отырған кездейсоқ шаманың үлестiрiм заңын қалыпты үлестiрiммен салыстыру үшiн Еk эксцесс және Аs асимметрия сипаттамалары қарастырылады. Мұнда
![]() ,
, ![]()
Ескерту : қалыпты үлестiрiм үшiн Ek = 0 , As = 0
Математикалық үмiттiң қасиеттерi
1. М(с) = с , 2. М(сх) = сМ(х)
3. М(х ± у) = М(х) ± М(у) 4. M(xy) = M(x)×M(y)
Дисперсияның қасиеттерi
1. D(x) ³ 0 , 2. D(c) = 0
3. D(cx) = c2 D(x) 4. D(x ± y) = D(x) + D(y)
Мұндағы x және y тәуелсiз кездейсоқ шамалар.
Жоғарыда келтiрiлген үлестiрiм заңдарының математикалық үмiттерi мен дисперсияларын келтiрелiк.
1. Биномдық үлестiрiм
M(x) = np, D(x) = npq, ![]() ,
, ![]()
2 Пуассон үлестiрiмi
M(x) = l, D(x) = l, ![]() ,
, ![]()
3. Геометриялық үлестiрiм
![]() ,
, ![]() (2.1.12)
(2.1.12)
4. Паскаль үлестiрiмi
![]() ,
, ![]()
5. Гипергеометриялық үлестiрiм
![]()
Мұнда m < 0,1×N болғанда D(x) » npq болады, яғни биномдық үлестiрiмнiң дисперсиясына жуықтап тең болады.
Сондықтан m < 0,1×N болғанда
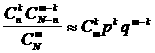
болады. Осы жағдайда ![]() болады.
болады.
Мысал 3. Дискреттi кездейсоқ шама мына үлестiрiммен берiлсiн
|
Х |
-1 |
0 |
1 |
2 |
|
р |
0,2 |
0,4 |
0,2 |
0,2 |
Сандық сипаттамаларын тап.
Шешуi :
М(X) = -1×0,2 + 0×0,4 + 1×0,2 + 2×0,2 = 0,4
Дисперсияны /2.1.8/ формуласын қолданып табамыз. Ол үшiн әуелi
|
X2 |
1 |
0 |
1 |
4 |
|
р |
0,2 |
0,4 |
0,2 |
0,2 |
жазамыз. Сонда ![]()
М0=0. Себебi кездейсоқ шаманың х=0 мәнi ең үлкен ықтималдықпен қабылданады. Ендi MD табу үшiн n = 4 екенiн ескерiп ![]() аламыз.
аламыз.
Сондай-ақ, жоғарыда келтiрiлген (2.1.9) - (2.1.11) формулаларын пайдаланып
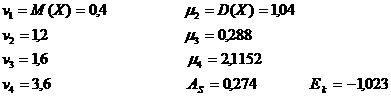
табамыз. Мұнда Аs > 0 олай болса дифференциалдық функцияның графигi оң жаққа ”созыңқы” , ал ![]() < 0 сондықтан бұл график Гаусс қисығына қарағанда ”жатыңқы”.
< 0 сондықтан бұл график Гаусс қисығына қарағанда ”жатыңқы”.
II-блок. үзіліссіз кездейсоқ шамалар
11-сабақ. Үлестірім заңдары
Анықтама. Егер кездейсоқ шама өзiнiң мүмкiн мәндерiн [a,b] интервалында қабылдаса және бұл мәндердi нөмiрлеуге болмаса, онда ол үзiлiссiз кездейсоқ шама деп аталады.
Мысалы поездың кешiгу уақыты, атылған оқтың ұшу алыстығы т.б. кездейсоқ шамалардың мүмкiн мәндерi белгiлi бiр интервалды қамтып жатады.
Кездейсоқ шаманың үлестiрiм заңдылықтарын әртүрлi жолмен қарастыруға болады. Төменде Х-кездейсоқ шаманың мүмкiн мәндерi тиянақты х санынан кiшi болу ықтималдығы қарастырылады.
Анықтама. Үлестiрiм функциясы деп Х-кездейсоқ шамасының мәндерi тиянақты х санынан кiшi болу ықтималдығын айтады.
Үлестiрiм функциясы F(x) арқылы белгiленедi. Сонда анықтама бойынша
F(x)=P(X<x)
Бұл функцияны сондай-ақ интегралдық үлестiрiм функциясы деп те атайды.
Негiзгi қасиеттерi:
1 P(a £ X £ b)=F(b)-F(a)
2 F(x2) ³ F(x1), x2³ x1 (2.2.1)
3 ![]()
![]()
Дискреттi кездейсоқ шама үшiн интегралдық үлестiрiм функция былай анықталады:
F(x)=P(X<x)= ![]() (2.2.2)
(2.2.2)
Мұндағы x1, x2 ... ,xn дискреттi кездейсоқ шаманың қабылдайтын мүмкiн мәндерi, ал p1,p2,...,Рn сол мәндердiң қабылдануының сәйкес ықтималдықтары. Мына (2.2.2) қоcындысы тек xi < x теңсiздiгiн қанағаттандыратын барлық xi үшiн олардың сәйкес ықтималдықтарының қосындысы болады; х берiлген тиянақты сан.
Анықтама: Үзiлiссiз кездейсоқ шаманың дифференциалдық функциясы (үлестiрiм тығыздығы) деп үлестiрiм функциясының бiрiншi туындысын айтады.
Дифференциалдық функцияны f(x) деп белгiлейдi. Сонда анықтама бойынша
f(x)=F ' (x (2.2.3)
Негiзгi қасиеттерi:
1. ![]()
2. ![]()
3 P(a£x£b)= 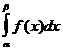
4. F(x)= 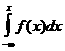
Мысал 1. Айталық Х - дискреттi кездейсоқ шама үлестiрiм кестесi арқылы берiлген болсын
|
Х |
0 |
1 |
3 |
3,5 |
|
Р |
0,1 |
0,4 |
0,2 |
0,3 |
Х - тiң үлестiрiм функциясын табыңыз.
Шешуi: Ол үшiн (2.2.2) формуласын пайдаланамыз. Кестеден байқағанымыздай х<0 болса, онда X-тiң қабылдайтын мүмкiн мәндерi жоқ. Ал 0 £ x <1 болғанда Х-тiң қабылдайтын бiр мәнi, ол - 0; ендi 1 £ x <3 болса, онда Х-тiң қабылдайтын екi мәнi бар, ол 0,1; т.с.с. ақырында х ³ 3,5 болса, онда Х өзiнiң барлық мүмкiн мәндерiн қабылдайды, ол - 0, 1, 3, 3, 5.
Ендi (2.2.2) формуласына түсiнiк келтiрелiк. Жоғарыда айтқанымыздай х<0 болса, онда есептiң шарты бойынша 0-санының сол жағында берiлген кездейсоқ шаманың ешбiр мүмкiн мәнi жоқ, яғни кездейсоқ шаманың өзiнiң мүмкiн мәндерiнiң бiреуiн қабылдауын оқиға екенiн ескерсек, онда оның 0-санының сол жағынан мән қабылдауы мүмкiн емес оқиға, олай болса
F(x) = P(x<0) = 0
Ендi x<1 болса,онда 1- санының сол жағында есептiң шарты бойынша кездейсоқ шаманың бiр мәнi бар, ол 0 - саны. Олай болса
F(x)=P(x<1)=P(x=0)=0,1
Сол сияқты x<3 болғанда, 3-санының сол жағында кездейсоқ шаманың екi мәнi бар. Ол осы мәндердiң бiреуiн қабылдауы мүмкiн, яғни екi оқиғаның бiреуi пайда болады дегенiмiз. Сондай-ақ, бұл екi оқиға үйлесiмсiз, сондықтан үйлесiмсiз оқиғалардың қосындысының ықтималдығы туралы теореманы пайдаланып:
F(x)=P(x<3)=P(x=0)+P(x=1)=0,1+0,4=0,5
Осы жолмен x<3,5 болғанда және x>3,5 болғандағы F(x)-ның мәндерiн есептеуге болады.
Сонымен қорытындысында:
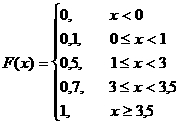
Ендi F(x) функциясының графигiн тұрғызайық.
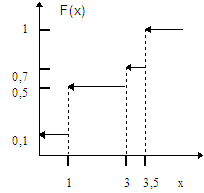
11.1 Бiрқалыпты үлестiрiм заңы
Анықтама. Егер Х - кездейсоқ шамасы [a,b] аралығында мән қабылдаса және оның үлестiрiм тығыздығы:
![]()
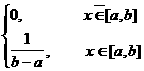 (2.2.12)
(2.2.12)
теңдiгi арқылы анықталса, онда ол кездейсоқ шама бiрқалыпты үлестiрiм заңымен берiлген дейдi.
Бұл үлестiрiм заңдылығы үшiн
![]()
![]() ,
, ![]()
![]() (2.2.13)
(2.2.13)
Интегралдық функциясы
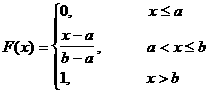 (2.2.14)
(2.2.14)
Берiлген аралықтан [c; d] мән қабылдау ықтималдығы
![]() (2.2.15)
(2.2.15)
Mысал 8. Кездейсоқ шама дифференциалдық функциясы арқылы берiлген
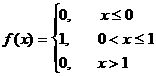
Интегралдық функцияны табыңыз. M(x), D(x)- тарды есептеңiз.
Шешуi: Есептiң шарты бойынша [0;1] аралығында f(x)=1 яғни тұрақты. Сондықтан бұл кездейсоқ шама бiрқалыпты үлестiрiм заңымен берiлген. Мұнда a=0, b=1.
Олай болса 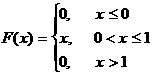
M(x)= ![]() =
= ![]() , D(x)=
, D(x)= ![]() ;
; ![]()
11.2 Көрсеткiштiк үлестiрiм заңы
Анықтама. Егер Х-кездейсоқ шамасы мына үлестiрiм тығыздығы
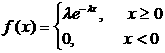 (2.2.16)
(2.2.16)
aрқылы берiлсе, онда ол көрсеткiштiк үлестiрiм заңымен берiлген дейдi.
Интегралдық функциясы
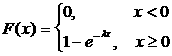 (2.2.17)
(2.2.17)
Бұл үлестiрiмнiң сандық сипаттамалары:
M(x)= ![]() , D(x)=
, D(x)= ![]() , s(x)=
, s(x)= ![]() ,
, ![]() (2.2.18)
(2.2.18)
Кездейсоқ шаманың ![]() аралығынан мән қабылдау ықтималдығы
аралығынан мән қабылдау ықтималдығы
![]() (2.2.19)
(2.2.19)
Мысал 10. Кездейсоқ шама интегралдық функциясы арқылы берiлген
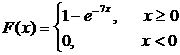
Математикалық үмiттi, дисперсияны табыңыз.
Шешуi: Әуелi ықтималдық тығыздығын табамыз
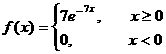
Бұдан M(x)= ![]() , D(x)=
, D(x)= ![]() , s(x)=
, s(x)= ![]()
11.3 Қалыпты үлестiрiм заңы
Анықтама. Егер Х - кездейсоқ шамасы мына үлестiрiм тығыздығы
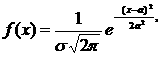 (2.2.20)
(2.2.20)

арқылы берiлсе, онда ол қалыпты үлестiрiм заңымен берiлген дейдi.
Мұнда M(x)=a, D(x)=s2, AS=0, Ek=0 (2.2.21)

Сондай-ақ ![]() (2.2.22)
(2.2.22)
қалыпты үлестiрiммен берiлген кездейсоқ шаманың берiлген интервалдан мән қабылдауының ықтималдығы, Ф(х) - Лаплас функциясы. Мына формула
![]() (2.2.23)
(2.2.23)
кездейсоқ шаманың өзiнiң математикалық үмiтiнен ауыткуының абсолют шамасы d - дан кiшi болуының ықтималдығын анықтайды.
Егер формулада d=3s болса, онда
![]()
немесе
![]() ,
,
яғни кездейсоқ шаманың өзiнiң математикалық үмiтiнен ауыткуының абсолют шамасы 3s - дан аспауының ықтималдығы бiрге өте жақын екенiн көрсетедi.
Осыдан үш сигма ережесi шығады:
Егер кездейсоқ шама қалыпты үлестiрiммен берiлсе, онда оның математикалық үмiттен ауытқуының абсолют шамасы үш орташа квадраттық ауытқудан аспайды.
Мысал 11. Станок-автомат ұзындығы 125 мм деталдар дайындайды. Олардың берiлген ұзындықтан ауыткуы 0,5 мм аспайды. Дайындалған деталдардың 7 процентi сапасыз. Деталь ұзындықтарын кездейсоқ шама ретiнде қарастырып және оны қалыпты үлестiрiм арқылы берiлген деп оның дисперсиясын табу керек.
Шешуi: Х-кездейсоқ шама-деталдар ұзындығы. Есептiң шарты бойынша деталдардың орташа ұзындығы 125 мм, олай болса М(х)=а=125 мм. Сондай-ақ дайындау кезiнде 124,5<x<125,5. Себебi берiлген ұзындықтан ауытқу 0,5 мм аспайды. Сондықтан a=124,5, b=125,5, s=? Ендi (2.2.23) формуласын пайдаланайық.
![]()
Есептiң шарты бойынша 7 процент деталдар сапасыз. Олай болса
![]() ;
; ![]() ,
,
яғни 0,93 ықтималдықпен сапалы деталдар дайындалады.
Ф(х)- функциясының кестесiнен
![]() теңдiгiнен
теңдiгiнен ![]() аламыз.
аламыз.
Осыдан s2=D(x)=0,078
Мысал 12. Кездейсоқ шама қалыпты үлестiрiммен берiлген және M(x)=30, D(x)=4. Mына теңсiздiктiң |x-30|<d ықтималдығы 0,8-ге тең болғанда d қандай болу керек?
Шешуi: Есептiң шарты бойынша
![]()
Осыдан ![]()
Кестеден ![]()
![]() .
.
12-сабақ. Үзіліссіз кездейсоқ шаманың сандық сипаттамалары
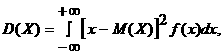 (2.2.5)
(2.2.5)
Жеңiлдетiлген формуласы:
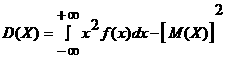 (2.2.6)
(2.2.6)
3. Орташа квадраттық ауытқуы
![]() (2.2.7)
(2.2.7)
4. К - реттi бастапқы моментi
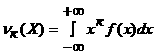 (2.2.8)
(2.2.8)
5. К - реттi орталық моментi
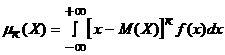 (2.2.9)
(2.2.9)
Үзiлiссiз кездейсоқ шамалардың мүмкiн мәндерi жөнiнде белгiлi дәрежеде информация беретiн басқада сипаттамалар бар. Оларға мода, медиана, асимметрия, эксцесстер жатады.
Анықтама. Егер кездейсоқ шаманың белгiлi бiр М0 мәнiнде ![]() теңдiгi орындалса, онда M0 кездейсоқ шаманың модасы деп аталады.
теңдiгi орындалса, онда M0 кездейсоқ шаманың модасы деп аталады.
Анықтама. Егер кездейсоқ шаманың белгiлi бiр MD мәнiнде
Р(x< MD)=P(x> MD) орындалса, онда MD кездейсоқ шаманың медианасы деп аталады.
Анықтама. Кездейсоқ шаманың өзiнiң математикалық үмiтi бойынша симметриядан ауыткуы, оның асимметриясы деп аталады және Аs деп белгiлейдi:
Аs=m3/ ![]() 3 (2.2.10)
3 (2.2.10)
Мұнда m3 - үшiншi реттi орталық момент, ![]() - орташа квадраттық ауыткуы.
- орташа квадраттық ауыткуы.
Егер кездейсоқ шаманың үлестiрiмi математикалық үмiтi бойынша симметриялы болса, онда As=0. Егер As>0, онда дифференциалдық функцияның графигi оң жаққа қарай "созыңқы" болады, ал As<0, онда - сол жаққа қарай "созыңқы" болады.
Анықтама. Қалыпты үлестiрiммен салыстырғанда дифференциалдық функцияның графигiнiң "жатыңқылық" деңгейiн анықтайтын шаманы эксцесс деп атайды және ![]() арқылы белгiлейдi:
арқылы белгiлейдi: ![]() (2.2.11)
(2.2.11)
Мұнда қалыпты үлестiрiм үшiн ![]() . Егер
. Егер ![]() , онда Гаусс қисығымен салыстырғанда график "көтерiңкi" болады, егер
, онда Гаусс қисығымен салыстырғанда график "көтерiңкi" болады, егер ![]() , онда график "жатыңқы" болады.
, онда график "жатыңқы" болады.
Мысал 3. Үзiлiссiз кездейсоқ шама дифференциалдық функциямен берiлген
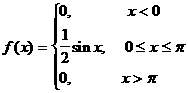
Кездейсоқ шаманың Мо, МD, As, Eк -ларын табу керек.
Шешуi: 1. Моданы табу үшiн f(x) функциясының максимумын табамыз. Ол үшiн әуелi бiрiншi туындыны тауып оны нөлге теңеп, сосын кризистiк нүкте тауып f(x)-тiң максимумын белгiлi схема бойынша анықтаймыз:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
Мұнда [0; p] кесiндiсiнде тек x= ![]() мәнi жатады. Ендi
мәнi жатады. Ендi
![]() (
( ![]() )=-
)=- ![]() <0. Осыдан
<0. Осыдан ![]() . Олай болса Mo=
. Олай болса Mo= ![]() .
.
Ендi медиананы табалық. Анықтамадан
![]()
Осыдан
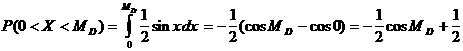
Сондай-ақ,
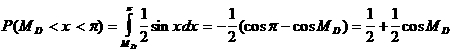
Осыдан ![]()
Ендi As және Eк-ларды табу үшiн әуелi
![]() ,
, ![]() ,
, ![]() ,
, ![]()
табамыз.
Сонда
![]() ,
, ![]() ,
, ![]()
Осы есептеулердi пайдаланып Аs=0 екенiн көремiз, яғни f(x) функциясының графигi өзiнiң M(x)-i бойынша симметриялы орналасқан.
Сол сияқты ![]()
екенiн көремiз, яғни f(x)-тiң графигi Гаусс кисығына қарағанда "жатыңқы" болады екен.
Мысал 4. Кездейсоқ шама дифференциалдық функциясы арқылы берiлген
f(x)= 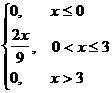
Интегралдық функциясын табыңыз.
Шешуi: Дифференциалдық функцияның төртiншi қасиетi бойынша
F(x)= 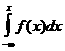
Осыдан x£0 болғанда f(x)=0 болатынын пайдаланып
F(x)= ![]() =0
=0
Ендi 0<x£3 болғанда f(x)= ![]() сондықтан
сондықтан
F(x)= 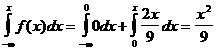
Ақырында x>3 болғанда f(x)=0 осыдан
F(x)= 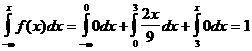
Сонымен
F(x)= 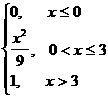
Мысал 5. Үзiлiссiз кездейсоқ шама үлестiрiм функциясымен берiлген
F(x)= 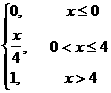
1 Үлестiрiм тығыздығын табу керек
2 M(x), D(x) табу керек
3 Мына интервалдан [ ![]() ,1] мән қабылдауының ықтималдығын табу керек.
,1] мән қабылдауының ықтималдығын табу керек.
Шешуi:
1. f(x)= 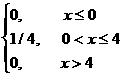
2. M(X)= 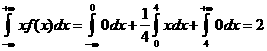
D(X)= ![]()
3. ![]()
III-блок. Кездейсоқ шамалар жүйелері. Кездейсоқ шамалар функциясы
13 сабақ. Үлестірім заңы. Кездейсоқ шамалар жүйесі. Шартты үлестірім. Сандық сипаттамалар
Бiр элементарлық кеңiстiкте X1, X2, ..., Xn кездейсоқ шамалар анықталған болсын. Сонда X1, X2, ..., Xn кездейсоқ шамалар системасы деп аталады, ал Z(X1, X2, ..., Xn) кездейсоқ вектор деп аталады, мұндағы X1, X2, ..., Xn оның координаталары болады.
Бiр өлшемдi кездейсоқ шамаларға қатысты негiзгi түсiнiктер мен анықтамалар көп өлшемдi кездейсоқ шамалар үшiн де сақталады.
Екi өлшемдi үзiлiссiз кездейсоқ шамалар үлестiрiм функциясы немесе дифференциалдық үлестiрiм функциясы арқылы анықталады.
Үлестiрiм функциясы X<x және У<y теңсiздiктерiнiң бiрмезгiлде орындалуының ықтималдығы ретiнде анықталады:
F(x,y)=P(X<x, У<y) (2.3.1)
Негiзгi қасиеттерi:
1. 0 £ F(x,y) £ 1
2. F(- ¥, y) = F(x, - ¥)=F(-¥,-¥)=0
3. F(¥,y)=F2(y)
4. F(x, ¥)=F1(x)
5. P(x1£X£x2, y1£У£y2)= [F(x2, y2)-F(x1, y2)] - [F(x2, y1)-F(x1, y1)]
Үзiлiссiз кездейсоқ шамалар үшiн
F(x,y)= 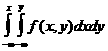 (2.3.2)
(2.3.2)
Мұнда f(x, y) - дифференциалдық үлестiрiм функциясы
![]()
Ал дискреттi кездейсоқ шамалар үшiн
![]() (2.3.3)
(2.3.3)
Егер ![]()
![]()
болса, онда Х және У тәуелсiз кездейсоқ шамалар деп аталады, дискреттi кездейсоқ шамалар үшiн тәуелсiздiк шарты
![]()
Екi өлшемдi дискреттi кездейсоқ шамалар кесте арқылы берiледi
1кесте|
У Х |
У1 |
у2 |
... |
уj |
... |
уn |
Рх |
|
х1 |
Р11 |
Р12 |
... |
Р1j |
... |
Р1n |
Рx1 |
|
х2 |
Р21 |
Р22 |
... |
Р2j |
... |
Р2n |
Рx2 |
|
|
... |
... |
... |
... |
... |
... |
... |
|
хi |
Рi1 |
Рi2 |
... |
Рij |
... |
Рin |
Рxi |
|
|
... |
... |
... |
... |
... |
... |
... |
|
хm |
Рm1 |
Рm2 |
... |
Рmj |
... |
Рmn |
Рxm |
|
Py |
Py1 |
Py2 |
... |
Pyj |
... |
Pyn |
1 |
Осы кестеден Х және У функцияларының үлестiрiм кестелерi былай жазылады:
2 кесте
|
Х |
х1 |
х2 |
... |
хi |
... |
хm |
|
Pх |
Рx1 |
Рx2 |
... |
Рxi |
... |
Рxm |
|
У |
у1 |
у2 |
... |
уj |
... |
уn |
|
Py |
Py1 |
Py2 |
... |
Pyj |
... |
Pyn |
Сондай-ақ, шартты ықтималдықтар төмендегi түрде анықталады:
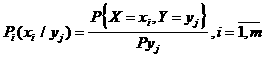
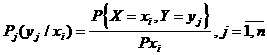
Cандық сипаттамалары:
М(х)= 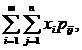 М(у)=
М(у)= 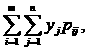
D(х)= ![]()
D(y)=
D(y)= 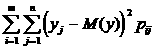
Cондай ақ екi өлшемдi кездейсоқ шамалар үшiн ковариация, корреляция коэффициенттерiнiң маңызы зор:
cov(x,y) = M ![]()
r(x,y) = ![]()
Осында, егер Х және У тәуелсiз кездейсоқ шамалар болса, r(x,y) = 0 болады.
Шартты математикалық үмiттер:
![]()
![]() ;
;
Мысал 1. Техникалық бақылау бөлiмi шығарылған бөлшектердiң стандарттылығын тексередi. Негiзгi тексерiлетiн параметрлер, олардың ұзындығы мен енi.
Сонда Х - детальдiң енiнiң стандарттан ауытқуы, У - ұзындығының стандарттан ауытқуы. Кездейсоқ шамалар кестемен берiлген
|
У Х |
-1 |
0 |
1 |
Рх |
|
-2 |
0,21 |
0,17 |
0,32 |
0,7 |
|
3 |
0,12 |
0,07 |
0,11 |
0,3 |
|
Ру |
0,33 |
0,24 |
0,43 |
1.00 |
1 Х және У кездейсоқ шамалардың үлестiрiм заңдарын жазыңыз.
2 а) Х-тiң У=y3 болғандағы шартты үлестiрiм заңын жазыңыз;
б) У-тiң Х=х2 болғандағы шартты үлестiрiм заңын жазыңыз;
3 Х пен У өзара тәуелсiз бе?
4 Үлестiрiм функциясын F(x,y) табыңыз:
Бiр өлшемдi Х және У кездейсоқ шамалардың үлестiрiм F1(x) және F2(y) функияларын жазыңыз.
5 Корреляциялық коэффициенттi табыңыз.
6 Шартты математикалық үмiттерiн табыңыз.
Шешуi: 1. кестеден Х және У кездейсоқ шамаларының үлестiрiм заңдары төмендегiдей түрде жазылды
2 кесте;|
Х |
-2 |
3 |
Рх |
0,7 |
0,3 |
3 кесте
|
У |
-1 |
0 |
1 |
Ру |
0,33 |
0,24 |
0,43 |
2. а) Х - тiң У=у3 болғандағы шартты үлестiрiм заңын жазу үшiн әуелi
![]() ,
, ![]() - тердi табамыз:
- тердi табамыз:
![]()
![]()
Сонда мына үлестiрiм заңын аламыз:
4 кесте|
Х |
-2 |
3 |
|
Р(Х/У=y3) |
32 43 |
11 43 |
б) У - тiң Х=х2 болғандағы шартты үлестiрiм заңын осылай есептесек:
5 кесте|
У |
-1 |
0 |
1 |
|
Р(У/Х=х2) |
12 30 |
7 30 |
11 30 |
3 Х және У тәуелсiз бе?
Екi Х және У кездейсоқ шамалардың өзара тәуелсiздiгiн анықтау үшiн олардың сәйкес шартты және шартсыз үлестiрiм заңдарын салыстыру керек. Егер ол заңдар бiрдей кестелермен берiлсе, онда олар тәуелсiз болғаны, ал егер ол кестелер бiрдей болмаса, онда олар тәуелдi болғаны. Сондықтан бiз N 2; N 4 және N 3; N 5 кестелердi өзара салыстырсақ, олардың бiрдей еместiгiн байқаймыз, олай болса Х және өзара тәуелдi кездейсоқ шамалар болады.
4 Үлестiрiм функциясын (2.3.3) формуланы пайдаланып жазамыз
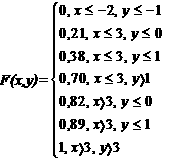
Ендi F1(x) және F2(y) функцияларын 2 кесте мен 3 кестенi пайдаланып табамыз:
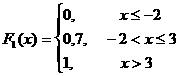
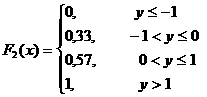 .
.
5. Корреляциялық коэффициенттi табалық
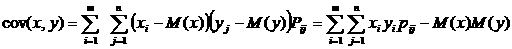
формуласын пайдаланып табалық.
Әуелi М(х) және М(у) - тердi 2 - 3 кестелердi пайдаланып табамыз.
М(х) = -2×0,7+3×0,3=-0,5, Д(х)=5,25, ![]()
M(y)=-1×0,33+0×0,24+1×0,43=0,1, Д(y)=0,87,
![]()
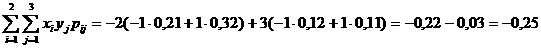
Сонда
![]() .
.
Осыдан ![]() екенiн көремiз, яғни Х және У өзара тәуелдi кездейсоқ шамалар болады.
екенiн көремiз, яғни Х және У өзара тәуелдi кездейсоқ шамалар болады.
6. Айталық М(Х/У=y3) және М(У/Х=х2) табу керек болсын. Оларды табу үшiн 4- 5 кестелердi пайдаланамыз. Сонда
![]()
![]() .
.
14-сабақ. Кездейсоқ шамалар функциясы
Кездейсоқ шамалар x1, x2, ..., xn системасын қарастыралық. Олардың әрқайсысының үлестiрiм заңдары белгiлi болсын. Сонда кездейсоқ шамалар функциясы мына түрде берiледi
y=j (x1, x2, ..., xn) (2.4.1)
Осы кездейсоқ шама y- тiң үлестiрiм заңын табу керек. Бiр кездейсоқ шаманың функциясын қарастыралық:
y=j(x) (2.4.2)
Мұнда Х дискреттi немесе үзiлiссiз кездейсоқ шама болуы мүмкiн.
1. Х - дискреттi кездейсоқ шама үлестiрiм кестесiмен берiлген.
Сонда у - кездейсоқ шаманың үлестiрiм заңы.
|
y |
j(x1) |
j(x2) |
... |
j(xn) |
|
P |
p1 |
P2 |
... |
Pn |
Мысал 3. Екi мерген бiр-бiрiнен тәуелсiз нысанаға сәйкес 2 және 3 атыс жасайды. Бiрiншiсiнiң нысанаға тигiзу ықтималдығы 0,9, ал екiншiсiнiкi - 0,8. X,Y - бiрiншi және екiншi мергеннiң нысанаға тигiзулерiнiң сандары. Z=X+Y, Z=X×Y кездейсоқ шамалардың үлестiрiм кестесiн жазыңыз. М(Х+У), М(X×У) - тердi табыңыз.
Шешуi: Х және У кездейсоқ шамалар биномдық үлестiрiм заңымен берiлген. Сондықтан Бернулли формуласын пайдаланып
|
Х |
0 |
1 |
2 | ||
|
Р |
0,01 |
0,18 |
0,81 |
|
У |
0 |
1 |
2 |
3 | |
|
Ру |
0,08 |
0,096 |
0,384 |
0,512 |
үлестiрiм кестелерiн аламыз.
Ендi Z=X+Y, Z= X×Y кездейсоқ шамаларының мүмкiн мәндерiн xi+yj және xi×yj табалық. Олардың ықтималдықтары P(X=xi)×P(У=yj) арқылы есептеледi. Ендi xi+yj және xi×yj мүмкiн мәндерiн есептелiк.
|
xi+yj |
x1+y1 |
x1+y2 |
x1+y3 |
x1+y4 |
x2+y1 |
x2+y2 |
x2+y3 |
x2+y4 |
|
xiyj |
x1y1 |
x1y2 |
x1y3 |
x1y4 |
x2y1 |
x2y2 |
x2y3 |
x2y4 |
|
P |
p1q1 |
p1q2 |
p1q3 |
p1q4 |
p2q1 |
p2q2 |
p2q3 |
p2q4 |
Осыдан
|
x+y |
0 |
1 |
2 |
3 |
4 |
5 |
|
P |
0,0008 |
0,0024 |
0,0276 |
0,152 |
0,4032 |
0,41472 |
|
xy |
0 |
1 |
2 |
3 |
4 |
6 |
|
P |
0,01792 |
0,01728 |
0,14688 |
0,09216 |
0,31104 |
0,41472 |
үлестiрiм заңдарын аламыз.
Сондай-ақ M(x+y)=4,2 M(x×y)=4,32006
Математикалық статистикада тәуелсiз қалыпты үлестiрiммен берiлген кездейсоқ шамалардың функциясы болып келетiн Үлестiрiм заңдарымен берiлген кездейсоқ шамалар қарастырылады. Солардың жиi кездесетiн үшеуiн төменде қарастырамыз.
1. Xu - квадрат үлестiрiм (c2- үлестiрiм). Айталық Х1, Х2, ..., Хn- тәуелсiз қалыпты кездейсоқ шамалар берiлсiн және a=0, s=1 болсын.
Ендi
c2n= x12+ x22+...+ xn2
кездейсоқ шаманы қарастыралық.
Бұл кездейсоқ шаманың үлестiрiм заңы c2 - үлестiрiм деп аталады. Мұнда n - еркiндiк дәрежелер саны деп аталады.
Жалпы жағдайда xк(к= ![]() ) қалыпты үлестiрiм параметрлерi а, s болса, онда
) қалыпты үлестiрiм параметрлерi а, s болса, онда ![]() алмастыруы арқылы параметрлерi (0,1) болатын қалыпты үлестiрiмге келтiруге болады, яғни
алмастыруы арқылы параметрлерi (0,1) болатын қалыпты үлестiрiмге келтiруге болады, яғни
c2n= ![]()
болады. c2 - үлестiрiмнiң кестесi барлық оқулықтарда келтiрiлген.
2. Стьюдент үлестiрiмi (t - үлестiрiм).
Айталық параметрлерi 0 және s болатын тәуелсiз қалыпты үлестiрiммен берiлген xi(i=![]() ) кездейсоқ шамалар болсын. Сонда Стьюдент үлестiрiмi мына түрде анықталады.
) кездейсоқ шамалар болсын. Сонда Стьюдент үлестiрiмi мына түрде анықталады.
.gif)
Мұнда n - еркiндiк дәрежелер саны.
Егер қалыпты үлестiрiмнiң параметрлерi а және s болса, онда xi-a кездейсоқ шамалары да тәуелсiз болады да, олардың параметрлерi сәйкес 0 және s болады. Сонда Стьюдент Үлестiрiмi төмендегiдей берiледi:
.gif)
Ал a=0, s =1 болса, онда Стьюдент үлестiрiмi
.gif)
болады, мұндағы ![]() жоғарында қарастырылған
жоғарында қарастырылған ![]() үлестiрiмi.
үлестiрiмi.
3. Фишер үлестiрiмi /F - үлестiрiмi/
Айталық параметрлерi (0,s) болатын тәуелсiз қалыпты үлестiрiммен берiлген кездейсоқ шамалар қарастырылсын:
![]()
Сонда мына функция арқылы берiлген кездейсоқ шаманы Фишер үлестiрiмi арқылы берiлген деп атайды:
.gif)
Егер xi - кездейсоқ шамалардың параметрлерi (a,s) болса, онда
Фишер үлестiрiмi төмендегiдей анықталады:
.gif)
Ал егер а=0, s=1 болса, онда Фишер үлестiрiмi былай жазылады:
.gif)
Мұндағы ![]() және
және ![]() кездейсоқ шамалары
кездейсоқ шамалары ![]() - үлестiрiммен берiлген.
- үлестiрiммен берiлген.
IV-блок. Үлкен сандар заңы
15-сабақ. Чебышев теңсіздігі
Үлкен сандар заңы бiрнеше теоремалар арқылы берiледi. Бұл теоремаларда (С.Чебышев, Бернулли; Пуассон теоремалары) өте көп кездейсоқ факторлардың жиынтық әсерi кездейсоқтықтан тәуелсiз нәтижелер алудың шарттары берiледi.
1 Чебышев теңсіздігі
Егер Х кездейсоқ шамасының дисперсиясы бар болса, онда мына теңсiздiктер орындалады:
![]() (2.5.1)
(2.5.1)
![]() (2.5.2)
(2.5.2)
мұндағы ![]()
Бұл теңсiздiктер кездейсоқ шаманың өзiнiң математикалық үмiтiнен ауытқуын бағалайды.
Мысал 1. Дискреттi кездейсоқ шама үлестiрiм заңымен берiлген
|
Х |
-1 |
0 |
2 |
4 |
6 |
|
Р |
0,2 |
0,4 |
0,3 |
0,05 |
0,05 |
1. Мына теңсiздiктiң |x-M(x)|<5 орындалуының ықтималдығын табыңыз.
2. Чебышев теңсiздiгiн пайдаланып |x-M(x)|<5 теңсiздiгiнiң орындалуының ықтималдығын бағалаңыз.
Шешуi: Әуелi математикалық үмiт, дисперсиясын табалық.
![]()
Ендi дисперсия табу үшiн Х2 - тың үлестiрiм заңын жазамыз:
|
Х2 |
1 |
0 |
4 |
16 |
36 |
|
Р |
0,2 |
0,4 |
0,3 |
0,05 |
0,05 |
Сонда:
![]()
![]()
1. Ендi |x-0,9|<5 теңсiздiгiнiң орындалу ықтималдығын табу үшiн осы теңсiздiктi қанағатандыратын Х-тiң мәндерiн анықтау қажет. Берiлген үлестiрiм кестесiмен бұл теңсiздiктi кездейсоқ шаманың x=-1, x=0, x=2, x=4 мәндерi қанағаттандыратынына көз жеткiзуге болады. Олай болса
![]()
0,2+0,4+0,3+0,05=0,95 ![]()
Сонымен
![]()
2. Чебышев теңсiздiгiн пайдаланып |x-0,9|<5 теңсiздiгiнiң орындалуын бағалайық:
![]()
яғни
![]() .
.
Сөйтiп Чебышев теңсiздiгiн пайдаланып |x-M(x)| ![]() 5 теңсiздiгiнiң орындалуының ықтималдығын төменнен бағаладық, яғни |x-0,9|
5 теңсiздiгiнiң орындалуының ықтималдығын төменнен бағаладық, яғни |x-0,9| ![]() 5 теңсiздiгi кем дегенде 0,8724 ықтималдықпен орындалады. Бұл тұжырымның құндылығы есептер шығарған кезде |x-M(x)| < e (e>0) теңсiздiгiнiң орындалуының дәл ықтималдығын табу мүмкiн болмаған жағдайларда оның ықтималдығын төменнен бағалауға мүмкiндiк бередi.
5 теңсiздiгi кем дегенде 0,8724 ықтималдықпен орындалады. Бұл тұжырымның құндылығы есептер шығарған кезде |x-M(x)| < e (e>0) теңсiздiгiнiң орындалуының дәл ықтималдығын табу мүмкiн болмаған жағдайларда оның ықтималдығын төменнен бағалауға мүмкiндiк бередi.
Мысал 2. Жарық берушi торға 20 электрошам параллель қосылған. Т уақыт iшiнде әрбiр шамның жарық беру ықтималдығы 0,8. Чебышев теңсiздiгiн пайдаланып Т уақытында жарық берушi барлық электрошамдармен, жарық берiп тұрған шамдардың арифметикалық орташа мәндерiнiң (математикалық үмiтi) айырмасының абсолюттiк шамасының ықтималдығын бағалаңыз. Егер айтылған айырма: 1) төрттен кiшi болса; 2) төрттен кем болмаса.
Шешуi: Белгiлi бiр Т уақытында жарық берiп тұрған электрошамдардың саны кездейсоқ шама. Бұл кездейсоқ шама биномдық үлестiрiм заңымен берiлген. Есептiң шарты бойынша n=20, p=0,8, q=0,2.
Сондықтан
M(x) = 20×0,8 = 16, D(x) = 16×0,2 = 3,2
Ендi Чебышев теңсiздiгiн пайдаланамыз
1. ![]()
2. ![]()
Сонымен
![]()
![]()
Мысал 3. Зауыт өнiмдерiнiң 75 процентiн жоғарғы сортпен шығарады. Шығарылған 100000 бұйымдардың iшiнде жоғарғы сортпен шығарылған бұйымдардың саны осы жоғарғы сортпен шығарылған бұйымдардың математикалық ұмiтiнен айырмасының абсолют шамасы 1000 данадан артық болмауының ықтималдығын бағалаңыз.
Шешуi: Жоғарғы сортпен шығарылған бұйымдар саны кездейсоқ шама. Оны Х арқылы белгiлейiк. Бұл кездейсоқ шама биномдық үлестiрiммен берiлген. М(х) осы кездейсоқ шаманың математикалық үмiтi. Есептiң шарты бойынша n=100000, P=0,75, q=0,25.
Сонда
М(х)=100000×0,75=75000, D(x)=18750
Осыдан
![]()
яғни
![]()
16-сабақ. Чебышев, Бернулли теоремалары
2.1 Чебышев теоремасы
Егер Х1, Х2, ..., Хn қос-қостан тәуелсiз кездейсоқ шамаларының ақырлы математикалық үмiттерi бар болып және дисперсиялары тұрақты С санымен шектелген болса, онда кез-келген n саны үшiн.
.gif) (2.1.1)
(2.1.1)
орындалады.
Бұл теореманы Чебышев теңсiздiгiн пайдаланып дәлелдегенде төмендегi бағалау алынады:
.gif) (2.1.2)
(2.1.2)
Егер М(хi)=а болса, онда (2.5.3) формула былай жазылады:
.gif) (2.1.3)
(2.1.3)
Чебышев теоремасының мағынасын түсiндiру үшiн мысал қарастырайық. Айталық белгiлi бiр бұйымның бiр өлшемi А болсын. Соны өлшеу керек. Өлшеу кезiнде әртүрлi себептерге байланысты қате кетедi. Сондықтан өлшеу кезiнде алынған нәтиже кездейсоқ шама болады. Бұл Х кездейсоқ шаманың математикалық үмiтi өлшеп отырған А шамасына тең болады, ал дисперсиясы D(x) пайдаланып отырған прибордың дәлдiгiн көрсетедi. Тәуелсiз n өлшеу жасалық.
Сонда x1, x2, ..., xn, сәйкес бiрiншi, екiншi, .... , n - шi өлшеулердiң нәтижелерi. Бұлардың өздерi кездейсоқ шамалар, олардың үлестiрiм заңдары Х-тiң үлестiрiм заңындай болады. Олай болса
![]()
кездейсоқ шамасыныңда үлестiрiм заңы сондай болады. Бiрақта n өскен сайын Х-тiң кездейсоқ сипаты бiрте-бiрте жоғала баcтайды да ол А-ға жақындай түседi. Х-тiң А-ға жақындағандығының шарттары Чебышев теоремасымен берiледi. Сонымен теореманың мағынасы:
|X-А|<e оқиғасы n мейлiнше үлкен болғанда ақиқат оқиға болады. Бұл теореманың практикалық маңызы мынада. Бiр нәрсенi өлшегенде мейлiнше дәл нәтиже алу үшiн оны бiрнеше рет өлшеп содан кейiн алған нәтижелердiң арифметикалық орташа мәнiн алу керек.
Мысал 1. Белгiлi бiр шаманың мәнi ретiнде мейлiнше көп өлшеулердiң арифметикалық орташа нәтижесi алынады. Әрбiр өлшеудiң мүмкiн мәндерiнiң орташа квадраттық ауытқуы 1 сантиметрден аспайды, деп қарастырып, 1000 өлшеуде алынған нәтиженiң берiлген шаманың шын мәнiнен ауытқуының абсолют шамасы 0,1 сантиметрден артық болмауының ықтималдығын бағалаңыз.
Шешуi: Әрбiр өлшеудiң нәтижесi кездейсоқ шама болады. Сондықтан 1000 өлшеудiң нәтижелерiн x1, x2, ..., x1000
тәуелсiз кездейсоқ шамалар жиынтығы ретiнде қарастырамыз. Сонда
![]()
100 өлшеудiң арифметикалық орташа мәнi болады. Ол да кездейсоқ шама болады. Ендi өлшеп отырған шаманың шын мәнiн а деп қабылдасақ. Чебышев теоремасын пайдалануға болады:
![]()
Cөйтiп ![]()
Мысал 2. Электрошамдар салынған 100 жәшiктiң әрқайсысынан олардың жану ұзақтығын анықтау үшiн бiр-бiрден электрошам алынды. Сөйтiп алынған шамдардың жану ұзақтығының арифметикалық орташа жану ұзақтығы есептелiндi. Осы арифметикалық орташа жану ұзақтығының жәшiктердегi барлық шамдардың жану ұзақтығының арифметикалық орташа жану ұзақтығынан айырмасының абсолют шамасының 2 сағаттан көп болмауының ықтималдығын бағалау керек. Шамдардың жану ұзақтығының орташа квадраттық ауытқуы 8 сағаттан аспайды.
Шешуi: Кездейсоқ шамаларға белгiлеу енгiзелiк. Хi i-iншi жәшiктен алынған электрошамның жану ұзақтығы, М(хi) - әр жәшiктегi шамдардың арифметикалық орташа жану ұзақтығы. Сонда
![]()
алынған шамдардың арифметикалық орташа жану ұзақтығы, ал
![]()
барлық шамдардың жану ұзақтығының арифметикалық орташа жану ұзақтығы. Сонымен есептiң шарты бойынша мына ықтималдықты бағалау керек.
![]()
Қарастырып отырған x1, x2, ..., x100 кездейсоқ шамалар үшiн Чебышев теоремасының шарттары орындалады. Олай болса
![]()
Сөйтiп
![]()
Mысал 3. Белгiлi бiр шаманы өлшегенде алынған нәтижелер дисперсиясы 1-ден аспайтын кездейсоқ шама. Осы нәтижелердiң арифметикалық орташа мәнiнiң берiлген шаманың шын мәнiн ауытқуының абсолют шамасы 0,01-ден артпауының ықтималдығы 0,98 - ден кем болмауы үшiн қанша өлшеу керек?
Шешуi: Әрбiр өлшеу кезiнде алынған нәтижелер кездейсоқ шама және олар тәуелсiз. Белгiлеу енгiзелiк
x1, x2, ..., xn
бiрiншi, екiншi, ... , n-шi өлшеулердiң нәтижелерi. Олай болса олардың арифметикалық орташа мәнi де
![]()
кездейсоқ шама. Ендi өлшеп отырған шаманың шын мәнiн а - деп белгiлесек, сонда бұл кездейсоқ шамалар Чебышев теоремасының шарттарын қанағаттандырады. Сондықтан
![]() .
.
Oсыдан мына теңсiздiктi аламыз:
![]()
Соңғы теңсiздiктi шешiп ![]() болатынын көремiз.
болатынын көремiз.
Мысал 4. Егер тәуелсiз x1, x2, ..., xn кездейсоқ шамалар тiзбегi төмендегiдей үлестiрiм заңымен берiлсе
|
Xn |
-3n |
0 |
3n |
|
P |
|
|
|
онда осы кездейсоқ шамалар тiзбегiне Чебышев теоремасын қолдануға бола ма?
Шешуi: Берiлген кездейсоқ шамалар тiзбегiне Чебышев теоремасын пайдалану үшiн бұл тiзбектер екi шартты қанағаттандыру керек:
1)Олар қос-қостан тәуелсiз болу керек.
2)Олардың математикалық үмiттерi ақырлы болып, дисперсиялары тұрақты бiр С санымен шектелген болуы керек.
Берiлген кездейсоқ шамалар үшiн бiрiншi шарт орындалады, себебi есептiң шарты бойынша олар тәуелсiз кездейсоқ шамалар. Ал екiншi шарттың орындалуын тексеру қажет. Әуелi математикалық үмiттердi есептейiк:
M(xn) = - ![]() +
+ ![]() =0
=0
Ендi хn2 үшiн үлестiрiм кестесiн жазайық.
|
Хn2 |
9n2 |
0 |
9n2 |
|
P |
|
|
|
Осыдан М(хn2) = ![]()
ақырында D(x)= ![]()
Cонымен М(хn) ақырлы болады да, ал D(xn) шектелген болады. Олай болса Чебышев теоремасын пайдалануға болады.
2.2 Бернулли теоремасы
Егер әрбiр тәуелсiз n сынақтарда А оқиғасы тұрақты р ықтималдықпен m рет пайда болса, онда кез-келген n үшiн
![]() (2.2.1)
(2.2.1)
орындалады.
Бұл теореманы Чебышев теңсiздiгiн пайдаланып дәлелдегенде төмендегi бағалауды аламыз:
![]() (2.2.2)
(2.2.2)
Мысал 5. Оқиға тәуелсiз сынақтарда тұрақты 0,2 ықтималдықпен пайда болады. Оқиғаның 900 сынақтарда пайда болу салыстырмалы жиiлiгiнiң осы оқиғаның ықтималдығынан ауытқуының абсолют шамасы 0,04-ден кем болатындығының ықтималдығын бағалаңыз.
Шешуi: Есептiң шарттары Бернулли теоремасының шаттарымен сәйкес келедi. Сондықтан n=900, р=0,2, q=0,8, e=0,04 екенiн ескерiп, iздеп отырған ықтималдықты бағалау үшiн (2.5.7) формуланы пайдаланамыз.
![]()
Осыдан ![]()
Mысал 6. А оқиғасының тәжiрибеде пайда болу ықтималдығы 0,75-ке тең. Осы тәжiрибелерде оқиғаның пайда болуы салыстырмалы жиiлiгiнiң оның ықтималдығынан ауытқуының абсолют шамасы 0,05-тен артық болмауының ықтималдығы 0,96-ға тең болу үшiн қанша тәжiрибе жасау керек?
Шешуi: Есептiң шарты бойынша
![]()
(2.5.7) формуладан
![]()
Осыдан n³1875.
Мысал 7. Зауыт дайындалған бұйымның 90 процентi бiрiншi сортқа жатады. Тексеруге 600 бұйым алынды. Тексеруге алынған бұйымдардың iшiндегi бiрiншi сортқа жататын бұйымдардың үлесiнiң оның ықтималдығынан ауытқуының абсолют шамасы ![]() -нен кем болуының ықтималдығы 0,99-ға тең болуы үшiн бұл ауытқу қандай болуы керек?
-нен кем болуының ықтималдығы 0,99-ға тең болуы үшiн бұл ауытқу қандай болуы керек?
Шешуi: Есептiң шартын пайдалансақ онда мына теңдiктi жазамыз
![]()
Осыдан
![]() ,
,
немесе e=0,12.
ЖАТТЫҒУ Е С Е П Т Е РІ
1. Екi атқыш нысанаға бiр-бiрден атыс жасады. Нысанаға тигiзу ықтималдығы бiрiншi атқыш үшiн 0,6 ал екiншiсiнiкi - 0,8. Кездейсоқ шама Х-нысанаға тигiзудiң саны. Осы кездейсоқ шаманың үлестiрiм кестесiн құрыңыз.
2. Нысанаға тигiзу ықтималдығы 2/3 тең. Үш атыс жасағанда нысанаға тию санының үлестiрiм кестесiн құрыңыз.
 III-ші Модуль. Математикалық статистика:
III-ші Модуль. Математикалық статистика: III МОДУЛЬ. Математикалық статистика:
Математикалық статистика
I-блок. Негізгі ұғымдар. Таңдамалық әдіс
17-сабақ. Бас жинақ. Таңдама жинақ
Математикалық статистикада дискреттi немесе үзiлiссiз сандық сипатты белгi Х, яғни, осы белгiнiң мүмкiн мәндерiнен тұратын бас жинақ зерттелiнедi. Оның бас орташа, бас дисперсия т.с.с. сандық сипаттамаларын табу мәселесi практикалық қажеттiлiктен туындайды.
Алайда, көп жағдайда бас жинақты толық анықтау мүмкiн емес, немесе оны анықтау көп жағдайда тиiмсiз болады. Сондықтан, осы бас жинақтан варианталар деп аталынатын x1,x2,...,xk элементтерiнен тұратын жиынша кездейсоқ терiлiп алынады. Бұл жиыншада x1 вариантасы n1 рет, x2 вариантасы n2 рет, т.т., xк вариантасы nк рет қайталануы мүмкiн. Онда осы жиыншаны былай жазып
|
xi |
x1 |
x2 |
x3 |
... |
xk |
|
ni |
n1 |
n2 |
n3 |
... |
nk |
вариациялық қатар түрiнде жазылған таңдама деймiз.
Мұндағы ni - xi вариантасының жиiлiгi деп, ал n= ![]() таңдаманың көлемi деп аталады.
таңдаманың көлемi деп аталады.
Ендi осы таңдаманың сандық сипаттамалары арқылы бас жинақты зерттеуге болады. Осы таңдамалық тәсiл - математикалық статистиканың негiзгi тәсiлi болып табылады.
18-сабақ. Таңдаманың сандық сипаттамалары. Үлестірім функциясы
а) Эмпирикалық функция
![]() (3.1.1)
(3.1.1)
Мұнда nx Х-тан кiшi болатын варианталардың жиiлiктерiнiң қосындысы. таңдаманың көлемi үлкен болғанда, осы функция арқылы бас жинақтың белгiсiз интегралдық үлестiрiм функциясы F(x) -ты жуықтап табуға болады.
б) Жиiлiктер полигоны.
Жазықтықтағы координаталары (x1,n1), (x2,n2),..., (xk,nk) нүктелерiн қосатын кесiндiлерден тұратын қисық сызық полигон деп аталады.
в) таңдамалық орташа
.gif) (3.1.2)
(3.1.2)
г) таңдамалық дисперсия
![]() (3.1.3)
(3.1.3)
д) таңдамалық орташа квадраттық ауытқу.
![]() (3.1.4) е) к-шы реттi бастапқы эмпирикалық момент
(3.1.4) е) к-шы реттi бастапқы эмпирикалық момент
Мк= ![]() , к=1,2,3,... (3.1.5)
, к=1,2,3,... (3.1.5)
ж) к -шы реттi орталық эмпирикалық момент
mк= .gif) к=1,2,3,.. (3.1.6)
к=1,2,3,.. (3.1.6)
з) таңдамалық асимметрия
.gif) (3.1.7)
(3.1.7)
и) таңдамалық эксцесс
![]() (3.1.8)
(3.1.8)
Ескерту 1. Егер Хi варианталары үлкен сандар болса, жоғарыдағы (3.1.3) формулаларын тiкелей пайдаланбай,ui = xi - c деген шартты варианталарға көшiп, мына формулаларды пайдаланған ыңғайлы болады
![]() (3.1.9)
(3.1.9)
.gif) (3.1.10)
(3.1.10)
Мұндағы С - "жалған нөл" деп аталынатын сан, оны өзiмiз жиiлiгi ең үлкен варианталарына шамалас етiп таңдаймыз.
Мысал 1. таңдама мына вариациялық қатар түрiнде берiлген:
|
xi |
1 |
4 |
5 |
|
ni |
4 |
4 |
2 |
Барлық сипаттамаларын табыңыз.
Шешуi: xi варианталары кiшкене сандар болғандықтан (3.1.1) - (3.1.8) формулаларын тiкелей қолданамыз.
а) таңдаманың көлемi n=10 және x £ 1 болса nx=0 (1-ден кiшi варианталар жоқ), демек F*(x)=0 , ал x<4 болса nx = 4, F*(x)=0,4, т.с.с. есептеулер жүргiзiп мына функцияны табамыз.
.gif)
Осы функцияның графигi төмендегiдей болғандықтан, эмпирикалық функцияны баспалдақ тәрiздес функция деп атау орынды.
.gif)
б) Жиiлiктер полигоны төмендегiдей қисық болады.
.gif)
в) ![]()
г) ![]()
д) ![]()
е) ![]()
ж) ![]() ,
, ![]()
![]()
![]()
з) ![]()
и) ![]()
Мысал 2. Берiлген вариациялық қатар арқылы хТ мен DT -ны табыңыз.
|
xi |
3860 |
3900 |
3910 |
3913 |
|
ni |
2 |
13 |
4 |
1 |
Шешуi: Варианталар үлкен сандар, сондықтан С=3900 деп алып, Ui=Xi-C шартты варианталарға көшейiк, яғни шартты вариациялық қатар аламыз.
|
Ui |
-40 |
0 |
10 |
13 |
|
ni |
2 |
13 |
4 |
1 |
Сонда (3.1.9), (3.1.10) формулаларын пайдалансақ
![]()
![]()
Ескерту 2. Егер сандық сипатты белгi Х үзiлiссiз таралған болса, оның бақыланған мәндерi кiретiн интервалды үзындықтары h болатындай бiрнеше кiшi интервалдарға бөлiп, әрбiр бөлiкте жататын варианталардың жиiлiктерiнiң қосындысы ni анықталады. Сонда табаны (xi;xi+1) кiшi интервал, ал биiктiгi ![]() болатын тiктөртбұрыштардан құралған фигураны - гистограмма деймiз.
болатын тiктөртбұрыштардан құралған фигураны - гистограмма деймiз.
Мысал 3. Мына таңдаманың гистограммасын құрыңыз.
|
Интервал нөмiрi |
Кiшi интервалдар |
Варианталардың жиiлiктерiнiң қосындысы |
Жиiлiктер тығыздығы |
|
i |
(xi ; xi+1) |
ni |
ni /h |
|
1 2 3 |
(1 ; 5) (5; 9) (9; 13) |
20 30 50 |
5 7,5 12,5 |
Шешуi: Абциссалар осiнде ұзындықтары 4 болатын берiлген интервалдарды саламыз. Ендi табандары осы интервалдар болатын ал биiктiктерi ![]() болатын тiктөртбұрыштарды саламыз.
болатын тiктөртбұрыштарды саламыз.
.gif)
Гисторамманың ауданы n кв.өлшем бiрлiгiне тең болады.
II-блок. Үлестірім параметрлерін бағалау
19-сабақ. Нүктелік бағалау
Дискреттi немесе үзiлiссiз сандық сипатты белгi Х-ың үлестiрiмiнiң белгiсiз параметрiн Ө деп белгiлейiк. Оның таңдама арқылы табылатын нүктелiк бағасы Ө* болсын. Әртүрлi таңдамалар үшiн өзгерiп отыратындықтан Ө* - кездейсоқ шама болады.
Анықтама 1. Егер М(Ө*)= Ө болса, онда Ө* жылжымаған баға деп аталады, ал басқа жағдайда жылжыған баға деп аталады.
Анықтама 2. Егер ![]() болса, онда Ө* орнықты баға деп аталады, бұл жерде n - таңдама көлемi.
болса, онда Ө* орнықты баға деп аталады, бұл жерде n - таңдама көлемi.
Сөйлем 1. Бас орташаның жылжымаған және орнықты нүктелiк бағасы таңдамалық орташа болады.
Сөйлем 2. Бас дисперсияның жылжыған бағасы таңдамалық дисперсия болады, ал жылжымаған бағасы түзетiлген таңдамалық дисперсия s2 болады, мұнда ![]() n - таңдама көлемi.
n - таңдама көлемi.
Мысал 1. Бас жинақтан мынадай таңдама алынған.
|
xi |
4 |
5 |
7 |
|
ni |
10 |
5 |
5 |
а) Бас орташаның жылжымаған бағасын табыңыз.
б) Бас дисперсияcының жылжымаған және жылжыған бағаларын табыңыз.
Шешуi:
а) таңдамалық орташа жылжымаған баға болады.
![]()
б) Жылжыған баға ретiнде DT, ал жылжымаған баға ретiнде s2 алынады
![]() ,
, ![]()
Моментер әдісі
Бұл әдiс бастапқы және орталық эмпирикалық моменттер өздерiне сәйкес бастапқы және орталық теориялық моменттердiң орнықты бағалары болатындығына негiзделген. Осы сәйкес моменттердi бiр-бiрiне теңестiре отырып, үлестiрiмнiң белгiсiз параметрiнiң нүктелiк бағалауларын табуға болады.
Мысал 1. Көрсеткiштiк үлестiрiмнiң ![]() белгiсiз параметрi l- ның нүктелiк бағасын табыңыз.
белгiсiз параметрi l- ның нүктелiк бағасын табыңыз.
Шешуi: Бастапқы I-шi реттi эмпирикалық және теориялық моменттердi теңестiремiз.
n1=M1
Көрсеткiштiк үлестiрiмнiң бiрiншi реттi бастапқы моментi
n1=M(x)= ![]() ,
ал M1=
,
ал M1=![]() болғандықтан
болғандықтан
![]() =
=
![]() теңдiгiн аламыз. Осыдан белгiсiз параметр l-ның нүктелiк бағасы l*=
теңдiгiн аламыз. Осыдан белгiсiз параметр l-ның нүктелiк бағасы l*= ![]() тең.
тең.
Мысал 2. Берiлген таңдама бойынша моменттер әдiсiн қолданып қалыпты үлестiрiмнiң
.gif)
белгiсiз a және s параметрлерiнiң нүктелiк бағасын табыңыз.
Шешуi: Бұл жағдайда екi а және s белгiсiз параметр болғандықтан бiрiншi, екiншi реттi теориялық және эмпирикалық моменттердi теңестiремiз.
n1=M1, m2=m2.
Ары қарай n1=M(x)=a, m2=D(x)= s2 және M1= ![]() , m2=DT екенiн eскерсек, онда мынадай нүктелiк бағалар аламыз
, m2=DT екенiн eскерсек, онда мынадай нүктелiк бағалар аламыз
a*= ![]() , s*=
, s*= ![]()
Мысал 3. Берiлген таңдамасының сипаттамалары арқылы моменттер әдiсiмен бiрқалыпты үлестiрiмнiң
.gif)
белгiсiз a және b параметрлерiнiң нүктелiк бағаларын табыңыз.
Шешуi: Бiрiншi және екiншi реттi эмпирикалық моменттердi теориялық моменттерге теңестiрейiк, яғни n1=M1, m2=m2.
Сонда n1=M(x)= ![]() , m2=D(x)=
, m2=D(x)= ![]() , M1=
, M1= ![]() , m2=DT екенiн ескере отырып мынадай теңдеулер системасын аламыз:
, m2=DT екенiн ескере отырып мынадай теңдеулер системасын аламыз:
.gif)
Осы системаны шеше отырып, a*= ![]() -
- ![]() , b*=
, b*= ![]() +
+ ![]() нүктелiк бағаларын табамыз.
нүктелiк бағаларын табамыз.
20-сабақ. Интервалдық бағалау
Бiр санмен ғана анықталатын нүктелiк баға, таңдаманың көлемi аз болғанда, өрескел қатеге соқтыруы мүмкiн, сондықтан бас жинақтың белгiсiз параметрiнiң интервалдық бағасын, яғни осы q параметрi жататындай (a,b) интервалын белгiлi бiр сенiмдiлiкпен айқындау мәселесiн қарастырайық.
Анықтама 1. q параметрiнiң q* бағасы бойынша сенiмдiлiгi (сенiмдiлiк ықтималдығы) деп ½q-q*½<d теңсiздiгiнiң орындалу ықтималдығы g- ны айтады, яғни Р(½q-q*½< d)=g, бұл жерде d - бағаның дәлдiгi.
Анықтама 2. (q*-d, q*+d) - интервалын g сенiмдiлiгiмен алынған сенiмдiлiк интервалы деп атайды.
Сөйлем 1. Қалыпты үлестiрiммен берiлген сандық сипатты белгi Х шаманың белгiсiз а математикалық үмiтiн таңдамалық орташа ![]() арқылы g сенiмдiлiгiмен бағалау үшiн мынадай сенiмдiлiк интервалдарын аламыз.
арқылы g сенiмдiлiгiмен бағалау үшiн мынадай сенiмдiлiк интервалдарын аламыз.
а) Егер s - бас орташа квадраттық ауытқу белгiлi болса, онда
![]() (4.4.1)
(4.4.1)
t-саны Ф(t) = ![]() -ға тең болатындай сан, оны
Лаплас функциясының мәндер кестесiнен аламыз.
-ға тең болатындай сан, оны
Лаплас функциясының мәндер кестесiнен аламыз.
б) Егер s - белгiсiз болса, онда
![]() (4.4.2)
(4.4.2)
Мұнда S - түзетiлген таңдамалық орташа квадраттық ауытқу, ![]() - шамасы кестеден анықталады.
- шамасы кестеден анықталады.
Сөйлем 2. Қалыпты үлестiрiммен берiлген Х-тың бас орташа квадраттық ауытқуы s -ны берiлген g сенiмдiлiгiмен бағалау үшiн мынадай сенiмдiлiк интервалдарын аламыз.
s(1-q)< s<s(1+q) , егер q<1 (4.4.3)
0<s<s(1+q) , егер q>1 (4.4.4)
Бұл жерде q=q(n,g) - кестеден алынады.
Мысал 1. Бас орташа квадраттық ауытқуы s = 5 болатын қалыпты үлестiрiммен берiлген бас жинақтан алынған көлемi n=25 таңдамадан ![]() =17 табылды. Бас жинақтың белгiсiз математикалық үмiтiн g=0,99 сенiмдiлiгiмен бағалайтын интервалын табыңыз.
=17 табылды. Бас жинақтың белгiсiз математикалық үмiтiн g=0,99 сенiмдiлiгiмен бағалайтын интервалын табыңыз.
Шешуi: (4.4.1) формуласын пайдаланамыз. Егер ![]() , онда кестеден t=2,57, яғни
, онда кестеден t=2,57, яғни
![]()
Ocыдан ![]() сенiмдiлiк интервалы.
сенiмдiлiк интервалы.
Мысал 2. Әлдебiр физикалық шама бiр құралмен 10 рет өлшенедi. Өлшеулердiң кездейсоқ қателерiнiң түзетiлген орташа квадраттық ауытқуы 0,5 - ке тең. Өлшеу құралының дәлдiгiн g=0,99 сенiмдiлiгiмен табыңыз.
Шешуi: Құралдың дәлдiгi өлшеуде жiберiлген кездейсоқ қателердiң бас орташа квадраттық ауытқуымен сипатталады, яғни бiзге s -ны бағалайтын сенiмдiлiк интервалын табу керек.
g=0,99, n=10 болса, кестеден q=1,08 олай болса, (4.4.4) формуласын пайдалана отырып 0<s<1,04 дәлдiктi анықтайтын сенiмдiлiк интервалын табамыз.
p class=MsoNormal style=' '>
III-блок. Статистикалық болжамдар
21-сабақ. Пирсон Хи-квадрат критерийі
Анықтама 1. Статистикалық болжам деп кездейсоқ шаманың үлестiрiмiнiң түрi немесе үлестiрiм параметрлерi туралы алдын-ала жасалатын болжамды айтады. Статистикалық болжам таңдаманың көмегiмен тексерiледi.
Алдымен нөлдiк болжам деп аталатын, тексерiлуге тиiс Но болжамы қарастырылады. Бұл болжамға қарсы болжамды альтернативтi деп атап, Н1 әрiпiмен белгiлеймiз. Мысалы: үлестiрiмнiң белгiсiз параметрi q туралы нөлдiк болжам былай болса Но: q= qо , онда Н1 : q ¹ qо (Н1: q>< qo).
Cтатистикалық болжамды тексеру барысында екi түрлi қате жiберуiмiз мүмкiн.
Бiрiншi тектi қате - Но болжамы жоққа шығарылып Н1 болжамы қабылданады, бiрақ негiзiнде Но дұрыс.
Екiншi тектi қате - Но болжамын қабылдаймыз, бiрақ негiзiнде Н1 болжамы дұрыс.
Анықтама 2. Бiрiншi тектi қате жiберу ықтималдығын маңыздылық деңгейi деймiз де, a әрiпiмен белгiлеймiз.
Болжамды тексерудiң жалпы схемасы:
1 Үлестiрiмi белгiлi статистикалық критерий деп аталатын F кездейсоқ шамасы енгiзiледi. Бұл шаманың әртүрлi еркiндiк дәрежелерi болып, ал үлестiрiмi қалыпты, хи - квадрат, Стьюдент, Фишер-Снедекорүлестiрiмдерiмен берiлуi мүмкiн.
2 таңдамалық (эмпирикалық) белгiлi деректерге сүйене отырып, критерийдiң бақыланатын мәнi Fбақ анықталады.
3 Берiлген a маңыздылық деңгейiнде F үлестiрiмiнiң сын нүктелерi кестесi арқылы, критерийдiң сындық мәнi - Fсын анықталады.
4 Егер Fбақ<Fсын болса, онда Но болжамын жоққа шығару негiз жоқ, ал егер Fбақ>Fсын болса, онда Но болжамы қабылданбайды.
Егер үлестiрiм заңы белгiсiз болса, онда "бас жинақ А заңы бойынша үлестiрiлген", - деген нөлдiк болжам келiсiмдiк критерийлерi арқылы тексерiледi. Олардың бiрнеше түрi бар: Пирсон критерийi, Колмогоров критерийi, Смирнов критерийi т.т.
Но: "бас жинақ қалыпты үлестiрiммен берiлген" деген болжамды тексеру үшiн Пирсонның келiсiмдiк ![]() критерийi қолданылады.
критерийi қолданылады.
Сонымен h қадамымен бiркелкi орналасқан таңдама берiлсiн
|
хi |
х1 |
х2 |
х3 |
... |
хm |
|
ni |
n1 |
n2 |
n3 |
... |
nm |
Ендi теориялық жиiлiктердi табамыз.
![]()
![]()
.gif)
немесе
![]()
Осыдан мына кесте анықталады:
|
Эмпирикалық жиiлiктер |
N1 |
n2 |
n3 |
... |
nm |
|
Теориялық жиiлiктер |
|
|
|
... |
|
Теориялық және эмпирикалық жиiлiктердiң бiр-бiрiнен ауытқуы кездейсоқ па, бақылаулар саны аз ба, әлде "бас жинақ қалыпты үлестiрiммен берiлген" деген нөлдiк болжам дұрыс емес пе? Осы сұрақтарға Пирсон критерийi жауап бередi.
Тексеру схемасы:
2. Статистикалық критерий ретiнде мына кездейсоқ шаманы аламыз
.gif) (5.2.1)
(5.2.1)
Бұл шама - еркiндiк дәрежесi к=s-1-r болатын, хи - квадрат үлестiрiмiмен таралған кездейсоқ шама. Мұнда s - таңдамадағы топтар саны, r - үлестiрiм параметрлерiнiң саны.
2. Берiлген деректерге сүйене отырып, критерийдiң бақыланатын мәнiн анықтаймыз.
![]()
.gif) (5.2.2)
(5.2.2)

3. Берiлген a маңыздылық деңгейiнде, хи - квадрат үлестiрiмнiң сын нүктелерi кестесi арқылы ![]() критерийдiң сындық мәнiн анықтаймыз.
критерийдiң сындық мәнiн анықтаймыз.
4. Егер ![]() <
< ![]() - нөлдiк болжамды жоққа шығаруға негiз жоқ, ал егер
- нөлдiк болжамды жоққа шығаруға негiз жоқ, ал егер ![]() >
> ![]() - нөлдiк болжам қабылданбайды.
- нөлдiк болжам қабылданбайды.
Мысал. 1. Эмпирикалық және теориялық жиiлiктер берiлген
|
Эмпирикалық жиiлiктер |
5 |
13 |
39 |
75 |
105 |
83 |
32 |
14 |
|
Теориялық жиiлiктер |
3 |
15 |
41 |
80 |
101 |
77 |
38 |
13 |
Берiлген a=0,05 маңыздылық деңгейiнде бас жинақтың қалыпты үлестiрiлгендiгi туралы болжамды тексерiңiз.
Шешуi: Критерийдiң бақыланатын мәнiн анықтау үшiн төмендегi кестенi құрамыз.
|
|
|
|
|
|
|
|
1 2 3 4 5 6 7 8 |
5 13 39 75 105 83 32 14 |
3 15 41 80 101 77 38 13 |
2 -2 -2 -2 4 6 -6 1 |
4 4 4 25 16 36 36 1 |
1,333 0,267 0,097 0,3125 0,158 0,468 0,947 0,077 |
|
|
Сонымен ![]() =3,66, ал критерийдiң еркiндiк дәрежесi к=s-1-r=5, себебi s = 8, r = 2 (қалыпты үлестiрiм екi параметр арқылы анықталады). Онда кестеден
=3,66, ал критерийдiң еркiндiк дәрежесi к=s-1-r=5, себебi s = 8, r = 2 (қалыпты үлестiрiм екi параметр арқылы анықталады). Онда кестеден ![]() (0,05; 5)=11,1. Сонымен
(0,05; 5)=11,1. Сонымен ![]() <
< ![]() - нөлдiк гипотезаны жоққа шығаруға негiз жоқ. Алдыңғы 1-мысалда теориялық және эмпирикалық жиiлiктер берiлген. Ендi тек эмпирикалық жиiлiктер белгiлi болғанда теориялық жиiлiктердi қалай есептеуге болатындығын көрсетелiк.
- нөлдiк гипотезаны жоққа шығаруға негiз жоқ. Алдыңғы 1-мысалда теориялық және эмпирикалық жиiлiктер берiлген. Ендi тек эмпирикалық жиiлiктер белгiлi болғанда теориялық жиiлiктердi қалай есептеуге болатындығын көрсетелiк.
Мысал 2. Интервалдық вариациялық қатар (III-тарау,1-кесте) мына түрде берiлген:
|
|
0-5 |
5-10 |
10-15 |
15-20 |
20-25 |
|
|
10 |
21 |
35 |
22 |
12 |
Пирсон критерийiн қолданып маңыздылық деңгейi ![]() болғанда сандық белгiнiң бақыланған мәндерiн пайдаланып “бас жинақ қалыпты үлестiрiммен берiлген” -деген нөлдiк болжамды тексерiңiз.
болғанда сандық белгiнiң бақыланған мәндерiн пайдаланып “бас жинақ қалыпты үлестiрiммен берiлген” -деген нөлдiк болжамды тексерiңiз.
Шешуi.
а) гистограмманың түрi
б) эмпирикалық ассиметрия мен экцесс мына теңсiздiктердi
![]() және
және ![]() қанағаттандыруы керек.
қанағаттандыруы керек.
Мұндағы
![]() ,
, ![]()
Қарастырып отырған мысал үшiн
![]() ,
, ![]() , ал
, ал ![]() ,
, ![]()
олай болса ![]() және
және ![]() .
.
Ендi гистограммаға қарасақ (III тарау, §1), оның түрi Гаусс қисығына ұқсас. Демек, бас жинақ қалыпты үлестiрiммен берiлген деп болжам жасауға негiз бар.
2. Ендi нөлдiк болжамды тексеру үшiн Пирсон критерийiн қолданамыз. Ол үшiн
![]() ,
, .gif) формулаларын қолданып теориялық жиiлiктердi есептеймiз.
формулаларын қолданып теориялық жиiлiктердi есептеймiз.
Белгiлеу енгiзелiк ![]() ,
,
Есептеу кестесiн құрамыз.
|
Интервалдар |
|
|
|
|
|
|
|
|
0-5 |
10 |
-2,23 |
-1,35 |
-0,4870 |
-0,4115 |
0,0755 |
8 |
|
5-10 |
21 |
-1,35 |
-0,48 |
-0,4115 |
-0,1844 |
0,2277 |
23 |
|
10-15 |
35 |
-0,48 |
0,39 |
-0,1844 |
0,1517 |
0,3361 |
34 |
|
15-20 |
22 |
0,39 |
1,27 |
0,1517 |
0,3980 |
0,2463 |
25 |
|
20-25 |
|
1,27 |
2,14 |
0,3980 |
0,4838 |
0,0858 |
|
![]() бақ есептеу үшiнде есептеу кестесiн жазған тиiмдi
бақ есептеу үшiнде есептеу кестесiн жазған тиiмдi
|
|
|
|
|
|
|
|
1 |
10 |
8 |
2 |
4 |
0,5 |
|
2 |
21 |
23 |
-2 |
4 |
0,17 |
|
3 |
35 |
34 |
1 |
1 |
0,03 |
|
4 |
22 |
25 |
-3 |
9 |
0,36 |
|
5 |
12 |
9 |
3 |
9 |
1 |
|
|
1,7 |
Сонда ![]() бақ=1,7.
бақ=1,7.
Ендi ![]() маңыздылық деңгейiнде
маңыздылық деңгейiнде ![]() еркiндiк дәрежесi бойынша
еркiндiк дәрежесi бойынша ![]() сын(0,05;2) кiтап соңындағы кестеден анықтаймыз:
сын(0,05;2) кiтап соңындағы кестеден анықтаймыз:
![]() сын(0,05;2)=6. Осыдан
сын(0,05;2)=6. Осыдан ![]() бақ<
бақ< ![]() сын екенiн көремiз. Демек, бас жинақтың қалыпты үлестiрiммен берiлгендiгi туралы нөлдiк болжамды қабылдамауға негiз жоқ.
сын екенiн көремiз. Демек, бас жинақтың қалыпты үлестiрiммен берiлгендiгi туралы нөлдiк болжамды қабылдамауға негiз жоқ.
Жаттығу есептері
1. Мына таңдаманың сипаттамаларын және эмпирикалық функциясын табыңыз.
|
xi |
-1 |
1 |
2 |
3 |
|
ni |
3 |
4 |
2 |
1 |
2. Қалыпты үлестiрiлген бас жинақтың орташа квадраттық ауытқуын s, таңдамалық орташасын ![]() , түзетiлген таңдамалық орташа квадраттық ауытқуын s, таңдама көлемiн n деп алып, белгiсiз математикалық үмiт а - ны бағалайтын сенiмдiлiк интервалдарын табыңыз.
, түзетiлген таңдамалық орташа квадраттық ауытқуын s, таңдама көлемiн n деп алып, белгiсiз математикалық үмiт а - ны бағалайтын сенiмдiлiк интервалдарын табыңыз.
а) s= 4, ![]() 10,2 , n=16, g=0,99
10,2 , n=16, g=0,99
б) s = 5, ![]() 16,8 , n=25, g=0,95
16,8 , n=25, g=0,95
в) s = 3, ![]() 12 , n=9, g=0,99
12 , n=9, g=0,99
г) s = 7,2, ![]() 10 , n=40, g=0,95
10 , n=40, g=0,95
