II МОДУЛЬ
КЕЗДЕЙСОҚ ШАМАЛАР
I-блок. Дискретті кездейсоқ шамалар
9-сабақ. Дискретті кездейсоқ шамалардың үлестірім заңы
Айталық элементарлық оқиғалар кеңiстiгi
![]() берiлсiн. Егер осы кеңiстiкте
анықталған Х(w) функциясы сандық мәндер қабылдап, кез-келген x үшiн мына ықтималдық
берiлсiн. Егер осы кеңiстiкте
анықталған Х(w) функциясы сандық мәндер қабылдап, кез-келген x үшiн мына ықтималдық
P(X<x)=P{w: X(w)<x}
анықталған болса, онда X{w} функциясын кездейсоқ шама деп атайды.
Кездейсоқ шамалар мен кездейсоқ оқиғаларды бiр-бiрiнен ажырата бiлген жөн. Анықтамадан байқап отырғанымыздай кездейсоқ шама мiндеттi түрде пайда болады, тек оның қандай мәндi қабылдайтыны алдын-ала белгiсiз. Ал кездейсоқ оқиғаның пайда болуының өзi кездейсоқ жай.
Мысалы, теңге лақтыру тәжiрибесiн қарастырайық. Осы тәжiрибеде кездейсоқ оқиға деп елтаңбаның немесе цифрдiң пайда болуын айтамыз, ал кездейсоқ шама ретiнде тәжiрибе нәтижесiнде елтаңбаның пайда болу санын қарастыруға болады. Бұл кездейсоқ шаманың мүмкiн мәндерi 0, 1, 2 ...,n, яғни тәжiрибе нәтижесiнде елтаңба мүлде пайда болмауы мүмкiн, немесе 1 рет, 2 рет, ..., n рет пайда болуы мүмкiн. Кездейсоқ шамалар дискреттi және үзiлiссiз болып бөлiнедi.
Кездейсоқ шамалардың кейбiр мысалдарын келтiрелiк:
1 Тәуелсiз n сынақтарда тұрақты ықтималдықпен А оқиғасының пайда болу саны;
2 Бiр цех өнiмдерiнiң iшiндегi сапасыз бұйымдар саны;
3 Снарядтың үшу алыстығы;
4 Телефон станциясына белгiлi бiр уақыт мерзiмiнде келiп түскен тапсырыстар саны, т.б.
Осы мысалдардан көрiп отырғанымыздай кездейсоқ шама тәжiрибенiң кездейсоқ нәтижесiнiң сандық сипаттамасы екенiн байқаймыз.
Анықтама. Кездейсоқ шаманың қабылдайтын мәндерiнiң саны ақырлы болса немесе тiзбек түрiнде жазылса, онда ондай кездейсоқ шамаларды дискреттi кездейсоқ шамалар деп атайды.
Дискреттi кездейсоқ шаманы анықтау үшiн үлестiрiм қатары - үлестiрiм кестесi құрылады.
|
Х |
x1 |
x2 |
x3 |
... |
xn |
|
p |
p1 |
p2 |
p3 |
... |
pn |
Кестенiң жоғары жолында кездейсоқ шаманың мүмкiн мәндерi, ал төменгi жолында - сол мәндердiң сәйкес ықтималдықтары келтiрiлген.
Мұнда
![]() .
.
9.1 БИНОМДЫҚ ҮЛЕСТIРIМ
Егер мүмкiн мәндерi 0,1,2,..., к , ... болып, ал осы мүмкiн мәндердi қабылдау Х=к ықтималдықтары Бернулли формуласымен анықталса
<
![]() (2.1.1)
(2.1.1)

онда кездейсоқ шама биномдық үлестiрiм заңымен берiлген деп аталады.
Сонымен биномдық үлестiрiм заңдылығымен берiлген дискреттi кездейсоқ шаманы - тұрақты ықтималдықты А оқиғасының n тәуелсiз сынақтарда пайда болуының саны ретiнде қарастыруға болады.
9.2
 ПУАССОН
ҮЛЕСТIРIМI
ПУАССОН
ҮЛЕСТIРIМI
Егер тәуелсiз сынақтарда n үлкен сан болса және р-ның шамасы аз болса, онда кездейсоқ шаманың мүмкiн мәндерiнiң сәйкес ықтималдықтарын Пуассон формуласымен
P(X=x)=Pn(к)»
![]() ,
l
=np (2.1.2)
,
l
=np (2.1.2)
есептеу керек.
Бұл жағдайда кездейсоқ шама Пуассондық үлестiрiм заңымен берiлген дейдi. Бернулли схемасына негiзделген тағыда басқа үлестiрiмдердi келтiрелiк.
9.3 ГЕОМЕТРИЯЛЫҚ ҮЛЕСТIРIМ
Айталық тәуелсiз сынақтарда Бернулли схемасы
қарастырылсын, мұнда P(A)=p. Сонда қатарынан (к-1) рет
![]() оқиғасы пайда болып, ал к
-шы ретте А оқиғасының пайда болу ықтималдығы
мына формуламен анықталады
оқиғасы пайда болып, ал к
-шы ретте А оқиғасының пайда болу ықтималдығы
мына формуламен анықталады
Г(к,р)=(1-р)к-1рm (2.1.3)
Ықтималдығы осы формуламен анықталған (к=1,2,3...,n) кездейсоқ шаманы геометриялық үлестiрiмiмен берiлген дейдi.
9.4 ПАСКАЛЬ ҮЛЕСТIРIМI
Тәуелсiз сынақтарда
![]() оқиғасы қатарынан к-1
рет пайда болып, сосын А оқиғасы m рет пайда болуының
ықтималдығы мына формуламен анықталады.
оқиғасы қатарынан к-1
рет пайда болып, сосын А оқиғасы m рет пайда болуының
ықтималдығы мына формуламен анықталады.
![]() (2.1.4)
(2.1.4)
Ықтималдығы осы формуламен анықталған кездейсоқ шама Паскаль үлестiрiмiмен берiлген дейдi. Геометриялық үлестiрiм Паскаль үлестiрiмiнiң жеке жағдайы, яғни m=1 болғанда геометриялық үлестiрiмдi аламыз.
9.5 ГИПЕРГЕОМЕТРИЯЛЫҚ ҮЛЕСТIРIМ
Егер X кездейсоқ шамасының мүмкiн мәндерi 0,1,2,3 ...к болып, ал сәйкес ықтималдықтары мына формуламен
![]() (2.1.5)
(2.1.5)
анықталса, онда кездейсоқ шама гипергеометриялық үлестiрiммен берiлген дейдi.
Мысал 1. Жәшiкте барлығы 10 шар бар, олардың 7 - i қара 3-i көк шарлар. Жәшiктен кез-келген 5 шар алынды. Сол 5 шардың үшеуi қара болуының ықтималдығы қандай?
Шешуi: Осындай мазмұнды есептi классикалық анықтаманы
және комбинаторикадағы қосу және көбейту
ережелерiн пайдаланып шығаруға болады. Бұл есептi солай
шығарса
![]()
![]() болады.
болады.
Ендi осы есептi жалпы түрде келтiрейiк.
Мысал 2. Жәшiкте барлығы N шарлар бар, оның iшiнде n қара шар бар, ал (N-n) - көк шарлар. Жәшiктен кез-келген m шар алынды. Сол алынған m шардың iшiнде к қара шар болуының ықтималдығы қандай?
Шешуi: x - жәшiктен алынған шарлар саны. Бұл кездейсоқ шаманың мүмкiн мәндерi 0, 1, 2, ..., m.
Жәшiктегi N шардан m
шарды әртүрлi
![]() жолмен алуға болады, ал n
қара шарлардан к шарды әртүрлi
жолмен алуға болады, ал n
қара шарлардан к шарды әртүрлi
![]() жолмен алуға болады, сонда
алынған m шардың iшiнде m-к көк шарлар
болғандықтан
барлық N-n көк
шарлардан m - к көк шарды
жолмен алуға болады, сонда
алынған m шардың iшiнде m-к көк шарлар
болғандықтан
барлық N-n көк
шарлардан m - к көк шарды
![]() жолмен алуға болады. Сонымен жәшiктен алынған
шардың к қара шарын
жолмен алуға болады. Сонымен жәшiктен алынған
шардың к қара шарын
![]() жолмен, ал қалған m-к
көк шарды
жолмен, ал қалған m-к
көк шарды
![]() жолмен алуға болады екен.
Олай болса комбинаторикадағы көбейту ережесiн қолдансақ, алынған
m шардың iшiнде к
- қара шар, m-к - көк шар болуы
жолмен алуға болады екен.
Олай болса комбинаторикадағы көбейту ережесiн қолдансақ, алынған
m шардың iшiнде к
- қара шар, m-к - көк шар болуы
![]() ×
×
![]() жолмен анықталады.
жолмен анықталады.
Сонда ықтималдықтың классикалық анықтамасы бойынша
![]()
болады.
Сөйтiп X-кездейсоқ шама гипергеометриялық үлестiрiммен берiлгенiне көз жеткiздiк.
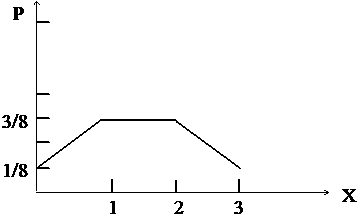
Мысал 3. Теңге үш рет лақтырылсын. Кездейсоқ шама Х ретiнде елтаңбаның пайда болу санын қарастырамыз.
1. Үлестiрiм қатарын жазу керек.
2. Үлестiрiм көпбұрышын салу керек.
3. M(x) , D(x) , s(х)-тарды табу керек.
Шешуi : Бұл кездейсоқ шама Х - тiң мүмкiн мәндерi 0, 1, 2, 3. Себебi теңгенi үш рет лақтырғанда елтаңба не пайда болмауы мүмкiн, не бiр рет пайда болуы мүмкiн т.с.с. Ал әрбiр лақтырғанда елтаңбаның пайда болу ықтималдығы 0,5 - ке тең. Олай дейтiнiмiз теңге лақтырғанда негiзiнен не елтаңба, не цифр пайда болады, ал теңгенiң симметриялығын ескерсек бұл екеуiнiң пайда болу ықтималдығы тең. Сондықтан бұл кездейсоқ шама Х- тi биномдық үлестiрiм заңымен сипаттауға болады.
Үлестiрiм қатарын жазайық:
|
Х |
0 |
1 |
2 |
3 |
|
Р |
|
|
|
|
немесе
|
Х |
0 |
1 |
2 |
3 |
|
Р |
1/8 |
3/8 |
3/8 |
1/8 |
Бұл жерде
![]() орындалады.
орындалады.
2 Үлестiрiм көпбұрышын салайық
3. Математикалық үмiттi (2.1.6) формуламен есептеймiз :
![]()
Ал дисперсияны әдетте жеңiлдетiлген (2.1.8) формуламен есептейдi. Ол үшiн х2 кездейсоқ шаманың үлестiрiм қатарын жазып алу керек.
|
Х2 |
0 |
1 |
4 |
9 |
|
р |
1/8 |
3/8 |
3/8 |
1/8 |
Сонда
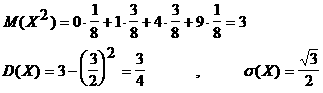
Сондай-ақ бұл мысалдағы кездейсоқ шаманың биномдық үлестiрiммен берiлгенiн ескерсек, онда сандық сипаттамаларды (2.1.12) формулаларын пайдаланып та есептеуге болады :
![]()
Мысал 4. Берiлген партияның 10 процентi сапасыз бұйымдар. Кез-келген 4 бұйым алынды. Осы төрт бұйымдардың iшiнде сапасыз бұйымдардың пайда болу санының үлестiрiм заңын жазу керек. Сандық сипаттамаларын есептеу керек.
Шешуi : Х- сапасыз бұйымдардың пайда болуының саны. Әрбiр сапасыз бұйымның пайда болу ықтималдығы 0,1-ге тең, себебi берiлген партияның 10 процентi сапасыз бұйымдар. Бұл кездейсоқ шама биномдық үлестiрiм заңымен берiлген. Мұнда
n =4, p = 0,1 , q = 0,9.
Сонда
|
Х |
0 |
1 |
2 |
|
3 |
|
Р |
|
|
|
|
|
немесе
|
Х |
0 |
1 |
2 |
3 |
4 |
|
Р |
0,6581 |
0,2916 |
0,0486 |
0,0036 |
0,0001 |
Ендi математикалық сипаттамаларын табайық
М(X) = 4×0,1=0,4 , D(X) = 4×0,1×0,9= 0,36 , s(X) = 0,6.
Мысал 5. Айталық 12 бұйымның 8-i бiрiншi сортқа жатады. Кез келген 5 бұйым алынды. Сонда осы 5 бұйымның iшiнде бiрiншi сортты бұйымдардың болуының үлестiрiм кестесiн құрыңыз.
Шешуi : Есептiң шарты бойынша N=12 , m=5 , n=8. Кездейсоқ шама Х. Оның мүмкiн мәндерi : 1, 2, 3, 4, 5. Мұнда мүмкiн мәндер бiрден басталуының себебi : 5 бұйымның iшiнде кем дегенде бiр бұйым бiрiншi сортқа жатады.
Сонда
![]()
Ендi үлестiрiм кестесiн жазалық
|
Х |
1 |
2 |
3 |
4 |
5 |
|
Р |
0,0101 |
0,1414 |
0,4242 |
0,3535 |
0,0707 |
10-сабақ. Дискретті кездейсоқ шамалардың сандық сипаттамалары
Дискреттi кездейсоқ шаманың математикалық үмiтi деп оның мүмкiн мәндерiнiң сәйкес ықтималдықтарына көбейтiндiлерiнiң қосындысын айтады:
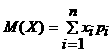 (2.1.6)
(2.1.6)
Дискреттi кездейсоқ шаманың дисперсиясы деп, оның өзiнiң математикалық үмiтiнен ауытқуының квадратының математикалық үмiтiн айтады:
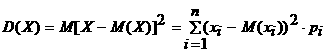 (2.1.7)
(2.1.7)
Дисперсияны есептеудiң жеңiлдетiлген формуласы :
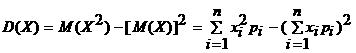 (2.1.8)
(2.1.8)
Дискреттi кездейсоқ шаманың орташа квадраттық ауытқуы мына формуламен есептелiнедi:
![]()
Дискреттi кездейсоқ шаманың бастапқы к - реттi моментi деп осы кездейсоқ шаманың к-шы дәрежесiнiң математикалық үмiтiн айтады:
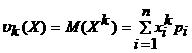 (2.1.9)
(2.1.9)
Дискреттi кездейсоқ шаманың к - реттi орталық моментi деп, оның өзiнiң математикалық үмiтiнен ауытқуының к-шы дәрежесiнiң математикалық үмiтiн айтады :
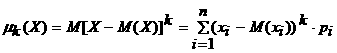 (2.1.10)
(2.1.10)
Кездейсоқ шаманың математикалық үмiтi бiрiншi бастапқы моментiне, ал дисперсиясы - екiншi орталық моментiне тең :
![]() ,
,
![]()
Сондай-ақ екiншi, үшiншi және төртiншi орталық моменттер
бастапқы моменттер арқылы төмендегiдей өрнектеледi :
![]() ,
,
![]() ,
,
![]() (2.1.11)
(2.1.11)
Дискреттi кездейсоқ шаманың ең ықтималды мәнiн оның Модасы (M0) деп атайды.
Айталық кездейсоқ шаманың n мүмкiн мәндерi болсын.
![]()
теңдiгi орындалса, онда
![]() кездейсоқ шаманың
медианасы деп аталады.
кездейсоқ шаманың
медианасы деп аталады.
Егер n=2к болса,
онда
![]() , егерде n=2к+1
болса, онда
, егерде n=2к+1
болса, онда
![]() ;
;
Сондай-ақ қарастырылып отырған кездейсоқ шаманың үлестiрiм заңын қалыпты үлестiрiммен салыстыру үшiн Еk эксцесс және Аs асимметрия сипаттамалары қарастырылады. Мұнда
![]() ,
,
![]()
Ескерту : қалыпты үлестiрiм үшiн Ek = 0 , As = 0
Математикалық үмiттiң қасиеттерi
1. М(с) = с , 2. М(сх) = сМ(х)
3. М(х ± у) = М(х) ± М(у) 4. M(xy) = M(x)×M(y)
Дисперсияның қасиеттерi
1. D(x) ³ 0 , 2. D(c) = 0
3. D(cx) = c2 D(x) 4. D(x ± y) = D(x) + D(y)
Мұндағы x және y тәуелсiз кездейсоқ шамалар.
Жоғарыда келтiрiлген үлестiрiм заңдарының математикалық үмiттерi мен дисперсияларын келтiрелiк.
1. Биномдық үлестiрiм
M(x)
= np, D(x)
= npq,
![]() ,
,
![]()
2 Пуассон үлестiрiмi
M(x) = l,
D(x) = l,
![]() ,
,
![]()
3. Геометриялық үлестiрiм
![]() ,
,
![]() (2.1.12)
(2.1.12)
4. Паскаль үлестiрiмi
![]() ,
,
![]()
5. Гипергеометриялық үлестiрiм
![]()
Мұнда m < 0,1×N болғанда D(x) » npq болады, яғни биномдық үлестiрiмнiң дисперсиясына жуықтап тең болады.
Сондықтан m < 0,1×N болғанда
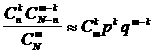
болады. Осы
жағдайда
![]() болады.
болады.
Мысал 3. Дискреттi кездейсоқ шама мына үлестiрiммен берiлсiн
|
Х |
-1 |
0 |
1 |
2 |
|
р |
0,2 |
0,4 |
0,2 |
0,2 |
Сандық сипаттамаларын тап.
Шешуi :
М(X) = -1×0,2 + 0×0,4 + 1×0,2 + 2×0,2 = 0,4
Дисперсияны /2.1.8/ формуласын қолданып табамыз. Ол үшiн әуелi
|
X2 |
1 |
0 |
1 |
4 |
|
р |
0,2 |
0,4 |
0,2 |
0,2 |
жазамыз. Сонда
![]()
М0=0. Себебi кездейсоқ шаманың х=0 мәнi
ең үлкен ықтималдықпен қабылданады. Ендi MD табу үшiн n = 4
екенiн ескерiп
![]() аламыз.
аламыз.
Сондай-ақ, жоғарыда келтiрiлген (2.1.9) - (2.1.11) формулаларын пайдаланып
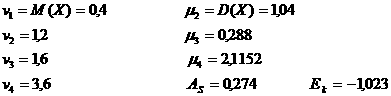
табамыз. Мұнда Аs > 0 олай болса
дифференциалдық
функцияның графигi оң жаққа ”созыңқы” , ал
![]() < 0
сондықтан бұл график
Гауссқисығына
қарағанда
”жатыңқы”.
< 0
сондықтан бұл график
Гауссқисығына
қарағанда
”жатыңқы”.
II-блок. үзіліссіз кездейсоқ шамалар
11-сабақ. Үлестірім заңдары
Анықтама. Егер кездейсоқ шама өзiнiң мүмкiн мәндерiн [a,b] интервалында қабылдаса және бұл мәндердi нөмiрлеуге болмаса, онда ол үзiлiссiз кездейсоқ шама деп аталады.
Мысалы поездың кешiгу уақыты, атылған оқтың ұшу алыстығы т.б. кездейсоқ шамалардың мүмкiн мәндерi белгiлi бiр интервалды қамтып жатады.
Кездейсоқ шаманың үлестiрiм заңдылықтарын әртүрлi жолмен қарастыруға болады. Төменде Х-кездейсоқ шаманың мүмкiн мәндерi тиянақты х санынан кiшi болу ықтималдығы қарастырылады.
Анықтама. Үлестiрiм функциясы деп Х-кездейсоқ шамасының мәндерi тиянақты х санынан кiшi болу ықтималдығын айтады.
Үлестiрiм функциясы F(x) арқылы белгiленедi. Сонда анықтама бойынша
F(x)=P(X<x)
Бұл функцияны сондай-ақ интегралдық үлестiрiм функциясы деп те атайды.
Негiзгi қасиеттерi:
1 P(a £ X £ b)=F(b)-F(a)
2 F(x2) ³ F(x1), x2³ x1 (2.2.1)
3
![]()
![]()
Дискреттi кездейсоқ шама үшiн интегралдық үлестiрiм функция былай анықталады:
![]() (2.2.2)
(2.2.2)
Мұндағы x1, x2 ... ,xn дискреттi кездейсоқ шаманың қабылдайтын мүмкiн мәндерi, ал p1,p2,...,Рn сол мәндердiң қабылдануының сәйкес ықтималдықтары. Мына (2.2.2) қоcындысы тек xi < x теңсiздiгiн қанағаттандыратын барлық xi үшiн олардың сәйкес ықтималдықтарының қосындысы болады; х берiлген тиянақты сан.
Анықтама: Үзiлiссiз кездейсоқ шаманың дифференциалдық функциясы (үлестiрiм тығыздығы) деп үлестiрiм функциясының бiрiншi туындысын айтады.
Дифференциалдық функцияны f(x) деп белгiлейдi. Сонда анықтама бойынша
f(x)=F ' (x (2.2.3)
Негiзгi қасиеттерi:
1.
![]()
2.
![]()
3
P(a£x£b)=
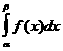
4. F(x)=
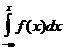
Мысал 1. Айталық Х - дискреттi кездейсоқ шама үлестiрiм кестесi арқылы берiлген болсын
|
Х |
0 |
1 |
3 |
3,5 |
|
Р |
0,1 |
0,4 |
0,2 |
0,3 |
Х - тiң үлестiрiм функциясын табыңыз.
Шешуi: Ол үшiн (2.2.2) формуласын пайдаланамыз. Кестеден байқағанымыздай х<0 болса, онда X-тiң қабылдайтын мүмкiн мәндерi жоқ. Ал 0 £ x <1 болғанда Х-тiң қабылдайтын бiр мәнi, ол - 0; ендi 1 £ x <3 болса, онда Х-тiң қабылдайтын екi мәнi бар, ол 0,1; т.с.с. ақырында х ³ 3,5 болса, онда Х өзiнiң барлық мүмкiн мәндерiн қабылдайды, ол - 0, 1, 3, 3, 5.
Ендi (2.2.2) формуласына түсiнiк келтiрелiк. Жоғарыда айтқанымыздай х<0 болса, онда есептiң шарты бойынша 0-санының сол жағында берiлген кездейсоқ шаманың ешбiр мүмкiн мәнi жоқ, яғни кездейсоқ шаманың өзiнiң мүмкiн мәндерiнiң бiреуiн қабылдауын оқиға екенiн ескерсек, онда оның 0-санының сол жағынан мән қабылдауы мүмкiн емес оқиға, олай болса
F(x) = P(x<0) = 0
Ендi x<1 болса,онда 1- санының сол жағында есептiң шарты бойынша кездейсоқ шаманың бiр мәнi бар, ол 0 - саны. Олай болса
F(x)=P(x<1)=P(x=0)=0,1
Сол сияқты x<3 болғанда, 3-санының сол жағында кездейсоқ шаманың екi мәнi бар. Ол осы мәндердiң бiреуiн қабылдауы мүмкiн, яғни екi оқиғаның бiреуi пайда болады дегенiмiз. Сондай-ақ, бұл екi оқиға үйлесiмсiз, сондықтан үйлесiмсiз оқиғалардың қосындысының ықтималдығы туралы теореманы пайдаланып:
F(x)=P(x<3)=P(x=0)+P(x=1)=0,1+0,4=0,5
Осы жолмен x<3,5 болғанда және x>3,5 болғандағы F(x)-ның мәндерiн есептеуге болады.
Сонымен қорытындысында:
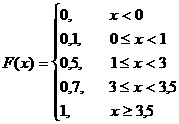
Ендi F(x) функциясының графигiн тұрғызайық.
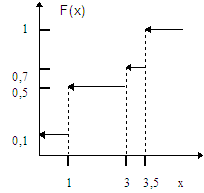
11.1 Бiрқалыпты үлестiрiм заңы
Анықтама. Егер Х - кездейсоқ шамасы [a,b] аралығында мән қабылдаса және оның үлестiрiм тығыздығы:
![]()
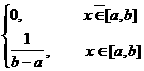 (2.2.12)
(2.2.12)
теңдiгi арқылы анықталса, онда ол кездейсоқ шама бiрқалыпты үлестiрiм заңымен берiлген дейдi.
Бұл үлестiрiм заңдылығы үшiн
![]()
![]() ,
-
,
-
![]()
![]() (2.2.13)
(2.2.13)
Интегралдық функциясы
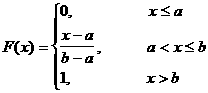 (2.2.14)
(2.2.14)
Берiлген аралықтан [c; d] мән қабылдау ықтималдығы
![]() (2.2.15)
(2.2.15)
Mысал 8. Кездейсоқ шама дифференциалдық функциясы арқылы берiлген
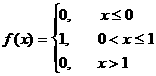
Интегралдық функцияны табыңыз. M(x), D(x)- тарды есептеңiз.
Шешуi: Есептiң шарты бойынша [0;1] аралығында f(x)=1 яғни тұрақты. Сондықтан бұл кездейсоқ шама бiрқалыпты үлестiрiм заңымен берiлген. Мұнда a=0, b=1.
Олай болса
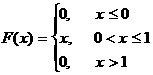
M(x)=
![]() =
=
![]() ,
,
D(x)=
![]() ;
;
![]()
11.2 Көрсеткiштiк үлестiрiм заңы
Анықтама. Егер Х-кездейсоқ шамасы мына үлестiрiм тығыздығы
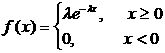 (2.2.16)
(2.2.16)
aрқылы берiлсе, онда ол көрсеткiштiк үлестiрiм заңымен берiлген дейдi.
Интегралдық функциясы
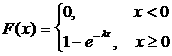 (2.2.17)
(2.2.17)
Бұл үлестiрiмнiң сандық сипаттамалары:
M(x)=
![]() ,Бик№Ю D(x)=
,Бик№Ю D(x)=
![]() , s(x)=
, s(x)=
![]() ,
,
![]() (2.2.18)
(2.2.18)
Кездейсоқ шаманың
![]() аралығынан мән
қабылдау ықтималдығы
аралығынан мән
қабылдау ықтималдығы
![]() (2.2.19)
(2.2.19)
Мысал 10. Кездейсоқ шама интегралдық функциясы арқылы берiлген
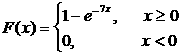
Математикалық үмiттi, дисперсияны табыңыз.
Шешуi: Әуелi ықтималдық тығыздығын табамыз
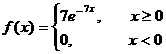
Бұдан M(x)=
![]() , D(x)=
, D(x)=
![]() , s(x)=
, s(x)=
![]()
11.3 Қалыпты үлестiрiм заңы
Анықтама. Егер Х - кездейсоқ шамасы мына үлестiрiм тығыздығы
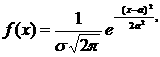 (2.2.20)
(2.2.20)

арқылы берiлсе, онда ол қалыпты үлестiрiм заңымен берiлген дейдi.
Мұнда M(x)=a, D(x)=s2, AS=0, Ek=0 (2.2.21)

Сондай-ақ
![]() (2.2.22)
(2.2.22)
қалыпты үлестiрiммен берiлген кездейсоқ шаманың берiлген интервалдан мән қабылдауының ықтималдығы, Ф(х) - Лаплас функциясы. Мына формула
![]() (2.2.23)
(2.2.23)
кездейсоқ шаманың өзiнiң математикалық үмiтiнен ауыткуының абсолют шамасы d - дан кiшi болуының ықтималдығын анықтайды.
Егер формулада d=3s болса, онда
![]()
немесе
![]() ,
,
яғни кездейсоқ шаманың өзiнiң математикалық үмiтiнен ауыткуының абсолют шамасы 3s - дан аспауының ықтималдығы бiрге өте жақын екенiн көрсетедi.
Осыдан үш сигма ережесi шығады:
Егер кездейсоқ шама қалыпты үлестiрiммен берiлсе, онда оның математикалық үмiттен ауытқуының абсолют шамасы үш орташа квадраттық ауытқудан аспайды.
Мысал 11. Станок-автомат ұзындығы 125 мм деталдар дайындайды. Олардың берiлген ұзындықтан ауыткуы 0,5 мм аспайды. Дайындалған деталдардың 7 процентi сапасыз. Деталь ұзындықтарын кездейсоқ шама ретiнде қарастырып және оны қалыпты үлестiрiм арқылы берiлген деп оның дисперсиясын табу керек.
Шешуi: Х-кездейсоқ шама-деталдар ұзындығы. Есептiң шарты бойынша деталдардың орташа ұзындығы 125 мм, олай болса М(х)=а=125 мм. Сондай-ақ дайындау кезiнде 124,5<x<125,5. Себебi берiлген ұзындықтан ауытқу 0,5 мм аспайды. Сондықтан a=124,5, b=125,5, s=? Ендi (2.2.23) формуласын пайдаланайық.
![]()
Есептiң шарты бойынша 7 процент деталдар сапасыз. Олай болса
![]() ;
;
![]() ,
,
яғни 0,93 ықтималдықпен сапалы деталдар дайындалады.
Ф(х)- функциясының кестесiнен
![]() теңдiгiнен
теңдiгiнен
![]() аламыз.
аламыз.
Осыдан s2=D(x)=0,078
Мысал 12. Кездейсоқ шама қалыпты үлестiрiммен берiлген және M(x)=30, D(x)=4. Mына теңсiздiктiң |x-30|<d ықтималдығы 0,8-ге тең болғанда d қандай болу керек?
Шешуi: Есептiң шарты бойынша
![]()
Осыдан
![]()
Кестеден
![]()
![]() .
.
12-сабақ. Үзіліссіз кездейсоқ шаманың сандық сипаттамалары
1. Математикалық үмiтi
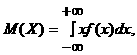 (2.2.4)
(2.2.4)
2. Дисперсиясы
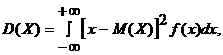 (2.2.5)
(2.2.5)
Жеңiлдетiлген формуласы:
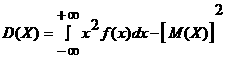 (2.2.6)
(2.2.6)
3. Орташа квадраттық ауытқуы
![]() (2.2.7)
(2.2.7)
4. К - реттi бастапқы моментi
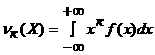 (2.2.8)
(2.2.8)
5. К - реттi орталық моментi
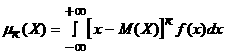 (2.2.9)
(2.2.9)
Үзiлiссiз кездейсоқ шамалардың мүмкiн мәндерi жөнiнде белгiлi дәрежеде информация беретiн басқада сипаттамалар бар. Оларға мода, медиана, асимметрия, эксцесстер жатады.
Анықтама.
Егер кездейсоқ шаманың белгiлi бiр М0 мәнiнде
![]() теңдiгi
орындалса, онда M0 кездейсоқ шаманың модасы деп аталады.
теңдiгi
орындалса, онда M0 кездейсоқ шаманың модасы деп аталады.
Анықтама. Егер кездейсоқ шаманың белгiлi бiр MD мәнiнде
Р(x< MD)=P(x> MD) орындалса, онда MD кездейсоқ шаманың медианасы деп аталады.
Анықтама. Кездейсоқ шаманың өзiнiң математикалық үмiтi бойынша симметриядан ауыткуы, оның асимметриясы деп аталады және Аs деп белгiлейдi:
Аs=m3/
![]() 3 (2.2.10)
3 (2.2.10)
Мұнда m3 - үшiншi
реттi орталық момент,
![]() - орташа
квадраттық ауыткуы.
- орташа
квадраттық ауыткуы.
Егер кездейсоқ шаманың үлестiрiмi математикалық үмiтi бойынша симметриялы болса, онда As=0. Егер As>0, онда дифференциалдық функцияның графигi оң жаққа қарай "созыңқы" болады, ал As<0, онда - сол жаққа қарай "созыңқы" болады.
Анықтама.
Қалыпты үлестiрiммен салыстырғанда
дифференциалдық функцияның графигiнiң
"жатыңқылық" деңгейiн анықтайтын шаманы
эксцесс деп атайды және
![]() арқылы белгiлейдi:
арқылы белгiлейдi:
![]() (2.2.11)
(2.2.11)
Мұнда
қалыпты үлестiрiм үшiн
![]() . Егер
. Егер
![]() , онда Гаусс
қисығымен салыстырғанда график "көтерiңкi"
болады, егер
, онда Гаусс
қисығымен салыстырғанда график "көтерiңкi"
болады, егер
![]() , онда график
"жатыңқы" болады.
, онда график
"жатыңқы" болады.
Мысал 3. Үзiлiссiз кездейсоқ шама дифференциалдық функциямен берiлген
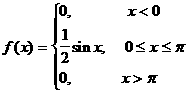
Кездейсоқ шаманың Мо, МD, As, Eк -ларын табу керек.
Шешуi: 1. Моданы табу үшiн f(x) функциясының максимумын табамыз. Ол үшiн әуелi бiрiншi туындыны тауып оны нөлге теңеп, сосын кризистiк нүкте тауып f(x)-тiң максимумын белгiлi схема бойынша анықтаймыз:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
Мұнда [0; p] кесiндiсiнде тек
x=
![]() мәнi жатады.
Ендi
мәнi жатады.
Ендi
![]() (
(
![]() )=-
)=-
![]() <0. Осыдан
<0. Осыдан
![]() . Олай болса Mo=
. Олай болса Mo=
![]() .
.
Ендi медиананы табалық. Анықтамадан
![]()
Осыдан
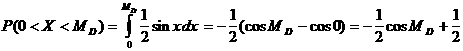
Сондай-ақ,
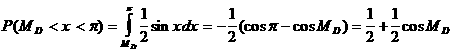
Осыдан
![]()
Ендi As және Eк-ларды табу үшiн әуелi
![]() ,
,
![]() ,
,
![]() ,
,
![]()
табамыз.
Сонда
![]() ,
,
![]() ,
,
![]()
Осы есептеулердi пайдаланып Аs=0 екенiн көремiз, яғни f(x) функциясының графигi өзiнiң M(x)-i бойынша симметриялы орналасқан.
Сол сияқты
![]()
екенiн көремiз, яғни f(x)-тiң графигi Гаусс кисығына қарағанда "жатыңқы" болады екен.
Мысал 4. Кездейсоқ шама дифференциалдық функциясы арқылы берiлген
f(x)=
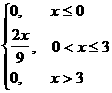
Интегралдық функциясын табыңыз.
Шешуi: Дифференциалдық функцияның төртiншi қасиетi бойынша
F(x)=
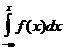
Осыдан x£0 болғанда f(x)=0 болатынын пайдаланып
F(x)=
![]() =0
=0
Ендi 0<x£3 болғанда f(x)=
![]() сондықтан
сондықтан
F(x)=
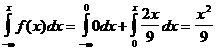
Ақырында x>3 болғанда f(x)=0 осыдан
F(x)=
\
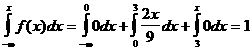
Сонымен
F(x)=
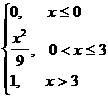
Мысал 5. Үзiлiссiз кездейсоқ шама үлестiрiм функциясымен берiлген
F(x)=
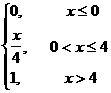
1 Үлестiрiм тығыздығын табу керек
2 M(x), D(x) табу керек
3
Мына
интервалдан [
![]() ,1] мән
қабылдауының ықтималдығын табу керек.
,1] мән
қабылдауының ықтималдығын табу керек.
Шешуi:
1. f(x)=
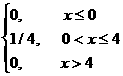
2. M(X)=
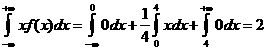
D(X)=
![]()
3.
![]()
III-блок. Кездейсоқ шамалар жүйелері. Кездейсоқ шамалар функциясы
13-сабақ. Үлестірім заңы. Кездейсоқ шамалар жүйесі. Шартты үлестірім. Сандық сипаттамалар
Бiр элементарлық кеңiстiкте X1, X2, ..., Xn кездейсоқ шамалар анықталған болсын. Сонда X1, X2, ..., Xn кездейсоқ шамалар системасы деп аталады, ал Z(X1, X2, ..., Xn) кездейсоқ вектор деп аталады, мұндағы X1, X2, ..., Xn оның координаталары болады.
Бiр өлшемдi кездейсоқ шамаларға қатысты негiзгi түсiнiктер мен анықтамалар көп өлшемдi кездейсоқ шамалар үшiн де сақталады.
Екi өлшемдi үзiлiссiз кездейсоқ шамалар үлестiрiм функциясы немесе дифференциалдық үлестiрiм функциясы арқылы анықталады.
Үлестiрiм функциясы X<x және У<y теңсiздiктерiнiң бiрмезгiлде орындалуының ықтималдығы ретiнде анықталады:
F(x,y)=P(X<x, У<y) (2.3.1)
Негiзгi қасиеттерi:
1. 0 £ F(x,y) £ 1
2 F(- ¥, y) = F(x, - ¥)=F(-¥,-¥)=0
3 F(¥,y)=F2(y)
4 F(x, ¥)=F1(x)
5 P(x1£X£x2, y1£У£y2)= [F(x2, y2)-F(x1, y2)] - [F(x2, y1)-F(x1, y1)]
Үзiлiссiз кездейсоқ шамалар үшiн
F(x,y)=
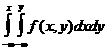 (2.3.2)
(2.3.2)
Мұнда f(x, y) - дифференциалдық үлестiрiм функциясы
![]()
Ал дискреттi кездейсоқ шамалар үшiн
![]() (2.3.3)
(2.3.3)
Егер
![]()
![]()
болса, онда Х және У тәуелсiз кездейсоқ шамалар деп аталады, дискреттi кездейсоқ шамалар үшiн тәуелсiздiк шарты
![]()
Екi өлшемдi дискреттi кездейсоқ шамалар кесте арқылы берiледi
1кесте
|
У Х |
У1 |
у2 |
... |
уj |
... |
уn |
Рх |
|
х1 |
Р11 |
Р12 |
... |
Р1j |
... |
Р1n |
Рx1 |
|
х2 |
Р21 |
Р22 |
... |
Р2j |
... |
Р2n |
Рx2 |
|
-
|
... |
... |
... |
... |
... |
... |
... |
|
хi |
Рi1 |
Рi2 |
... |
Рij |
... |
Рin |
Рxi |
|
|
... |
... |
... |
... |
... |
... |
... |
|
хm |
Рm1 |
Рm2 |
... |
Рmj |
... |
Рmn |
Рxm |
|
Py |
Py1 |
Py2 |
... |
Pyj |
... |
Pyn |
1 |
Осы кестеден Х және У функцияларының үлестiрiм кестелерi былай жазылады:
|
Х |
х1 |
х2 |
... |
хi |
... |
хm |
|
Pх |
Рx1 |
Рx2 |
... |
Рxi |
... |
Рxm |
|
|
|
|
|
|
|
|
|
У |
у1 |
у2 |
... |
уj |
... |
уn |
|
Py |
Py1 |
Py2 |
... |
Pyj |
... |
Pyn |
Сондай-ақ, шартты ықтималдықтар төмендегi түрде анықталады
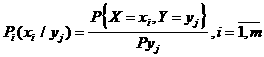
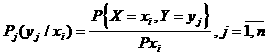
Cандық сипаттамалары
М(х)=
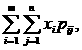 М(у)=
М(у)=
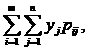
D(х)=
![]() D(y)=
D(y)=
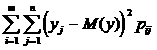
Cондай ақ екi өлшемдi кездейсоқ шамалар үшiн ковариация, корреляция коэффициенттерiнiң маңызы зор:
cov(x,y)
= M
![]()
r(x,y)
=
![]()
Осында, егер Х және У тәуелсiз кездейсоқ шамалар болса, r(x,y) = 0 болады.
Шартты математикалық үмiттер:
![]()
![]() ;
;
Мысал 1. Техникалық бақылау бөлiмi шығарылған бөлшектердiң стандарттылығын тексередi. Негiзгi тексерiлетiн параметрлер, олардың ұзындығы мен енi. Сонда Х - детальдiң енiнiң стандарттан ауытқуы, У - ұзындығының стандарттан ауытқуы. Кездейсоқ шамалар кестемен берiлген
1 кесте|
У Х |
-1 |
0 |
1 |
Рх |
|
-2 |
0,21 |
0,17 |
0,32 |
0,7 |
|
3 |
0,12 |
0,07 |
0,11 |
0,3 |
|
Ру |
0,33 |
0,24 |
0,43 |
1.00 |
1 Х және У кездейсоқ шамалардың үлестiрiм заңдарын жазыңыз.
2 а) Х-тiң У=y3 болғандағы шартты үлестiрiм заңын жазыңыз;
б) У-тiң Х=х2 болғандағы шартты үлестiрiм заңын жазыңыз;
3 Х пен У өзара тәуелсiз бе?
4 Үлестiрiм функциясын F(x,y) табыңыз:
Бiр өлшемдi Х және У кездейсоқ шамалардың үлестiрiм F1(x) және F2(y) функияларын жазыңыз.
5 Корреляциялық коэффициенттi табыңыз.
6 Шартты математикалық үмiттерiн табыңыз.
Шешуi: 1. кестеден Х және У кездейсоқ шамаларының үлестiрiм заңдары төмендегiдей түрде жазылды
2 кесте|
Х |
-2 |
3 |
|
|
Рх |
0,7 |
0,3 |
|
3 кесте
|
У |
-1 |
0 |
1 |
|
|
|
Ру |
0,33 |
0,24 |
0,43 |
2. а) Х - тiң У=у3 болғандағы шартты үлестiрiм заңын жазу үшiн әуелi
![]() ,
,
![]() - тердi табамыз:
- тердi табамыз:
![]()
![]()
Сонда мына үлестiрiм заңын аламыз:
4 кесте|
Х |
-2 |
3 |
|
Р(Х/У=y3) |
32 43 |
11 43 |
б) У - тiң Х=х2 болғандағы шартты үлестiрiм заңын осылай есептесек:
5 кесте|
У |
-1 |
0 |
1 |
|
Р(У/Х=х2) |
12 30 |
7 30 |
11 30 |
3 Х және У тәуелсiз бе?
Екi Х және У кездейсоқ шамалардың өзара тәуелсiздiгiн анықтау үшiн олардың сәйкес шартты және шартсыз үлестiрiм заңдарын салыстыру керек. Егер ол заңдар бiрдей кестелермен берiлсе, онда олар тәуелсiз болғаны, ал егер ол кестелер бiрдей болмаса, онда олар тәуелдi болғаны. Сондықтан бiз N 2; N 4 және N 3; N 5 кестелердi өзара салыстырсақ, олардың бiрдей еместiгiн байқаймыз, олай болса Х және өзара тәуелдi кездейсоқ шамалар болады.
4 Үлестiрiм функциясын (2.3.3) формуланы пайдаланып жазамыз
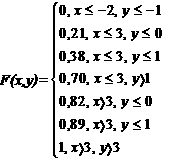
Ендi F1(x) және F2(y) функцияларын 2 кесте мен 3 кестенi пайдаланып табамыз:
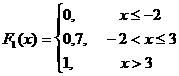
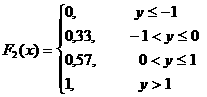 .
.
5. Корреляциялық коэффициенттi табалық
![]()
формуласын пайдаланып табалық.
Әуелi М(х) және М(у) - тердi 2 - 3 кестелердi пайдаланып табамыз.
М(х)
= -2×0,7+3×0,3=-0,5, Д(х)=5,25,
![]()
M(y)=-1×0,33+0×0,24+1×0,43=0,1, Д(y)=0,87,
![]()
![]()
Сонда
![]() .
.
Осыдан
![]() екенiн көремiз, яғни Х және
У өзара тәуелдi кездейсоқ шамалар болады.
екенiн көремiз, яғни Х және
У өзара тәуелдi кездейсоқ шамалар болады.
6. Айталық М(Х/У=y3) және М(У/Х=х2) табу керек болсын. Оларды табу үшiн 4- 5 кестелердi пайдаланамыз. Сонда
![]()
![]() .
.
14-сабақ. Кездейсоқ шамалар функциясы
Кездейсоқ шамалар x1, x2, ..., xn системасын қарастыралық. Олардың әрқайсысының үлестiрiм заңдары белгiлi болсын. Сонда кездейсоқ шамалар функциясы мына түрде берiледi
y=j (x1, x2, ..., xn) (2.4.1)
Осы кездейсоқ шама y- тiң үлестiрiм заңын табу керек. Бiр кездейсоқ шаманың функциясын қарастыралық:
y=j(x) (2.4.2)
Мұнда Х дискреттi немесе үзiлiссiз кездейсоқ шама болуы мүмкiн.
1. Х - дискреттi кездейсоқ шама үлестiрiм кестесiмен берiлген.
Сонда у - кездейсоқ шаманың үлестiрiм заңы.
|
y |
j(x1) |
j(x2) |
... |
j(xn) |
|
P |
p1 |
P2 |
... |
Pn |
Мысал 3. Екi мерген бiр-бiрiнен тәуелсiз нысанаға сәйкес 2 және 3 атыс жасайды. Бiрiншiсiнiң нысанаға тигiзу ықтималдығы 0,9, ал екiншiсiнiкi - 0,8. X,Y - бiрiншi және екiншi мергеннiң нысанаға тигiзулерiнiң сандары. Z=X+Y, Z=X×Y кездейсоқ шамалардың үлестiрiм кестесiн жазыңыз. М(Х+У), М(X×У) - тердi табыңыз.
Шешуi: Х және У кездейсоқ шамалар биномдық үлестiрiм заңымен берiлген. Сондықтан Бернулли формуласын пайдаланып
|
Х |
0 |
1 |
2 |
|
|
Р |
0,01 |
0,18 |
0,81 |
|
|
У |
0 |
1 |
2 |
3 |
|
Ру |
0,08 |
0,096 |
0,384 |
0,512 |
үлестiрiм кестелерiн аламыз.
Ендi Z=X+Y, Z= X×Y кездейсоқ шамаларының мүмкiн мәндерiн xi+yj және xi×yj табалық. Олардың ықтималдықтары P(X=xi)×P(У=yj) арқылы есептеледi. Ендi xi+yj және xi×yj мүмкiн мәндерiн есептелiк.
|
xi+yj |
x1+y1 |
x1+y2 |
x1+y3 |
x1+y4 |
x2+y1 |
x2+y2 |
x2+y3 |
x2+y4 |
|
xiyj |
x1y1 |
x1y2 |
x1y3 |
x1y4 |
x2y1 |
x2y2 |
x2y3 |
x2y4 |
|
P |
p1q1 |
p1q2 |
p1q3 |
p1q4 |
p2q1 |
p2q2 |
p2q3 |
p2q4 |
Осыдан
|
x+y |
0 |
1 |
2 |
3 |
4 |
5 |
|
P |
0,0008 |
0,0024 |
0,0276 |
0,152 |
0,4032 |
0,41472 |
|
xy |
0 |
1 |
2 |
3 |
4 |
6 |
|
P |
0,01792 |
0,01728 |
0,14688 |
0,09216 |
0,31104 |
0,41472 |
үлестiрiм заңдарын аламыз.
Сондай-ақ M(x+y)=4,2 M(x×y)=4,32006
Математикалық статистикада тәуелсiз қалыпты үлестiрiммен берiлген кездейсоқ шамалардың функциясы болып келетiн Үлестiрiм заңдарымен берiлген кездейсоқ шамалар қарастырылады. Солардың жиi кездесетiн үшеуiн төменде қарастырамыз.
1. Xu - квадрат үлестiрiм (c2- үлестiрiм). Айталық Х1, Х2, ..., Хn- тәуелсiз қалыпты кездейсоқ шамалар берiлсiн және a=0, s=1 болсын.
Ендi
c2n= x12+ x22+...+ xn2
кездейсоқ шаманы қарастыралық.
Бұл кездейсоқ шаманың үлестiрiм заңы c2 - үлестiрiм деп аталады. Мұнда n - еркiндiк дәрежелер саны деп аталады.
Жалпы
жағдайда xк(к=
![]() ) қалыпты үлестiрiм
параметрлерi а, s болса, онда
) қалыпты үлестiрiм
параметрлерi а, s болса, онда
![]() алмастыруы арқылы параметрлерi (0,1)
болатын қалыпты үлестiрiмге келтiруге болады, яғни
алмастыруы арқылы параметрлерi (0,1)
болатын қалыпты үлестiрiмге келтiруге болады, яғни
c2n=
![]()
болады. c2 - үлестiрiмнiң кестесi барлық оқулықтарда келтiрiлген.
2. Стьюдент үлестiрiмi (t - үлестiрiм).
Айталық параметрлерi 0
және s
болатын тәуелсiз қалыпты үлестiрiммен берiлген xi
(i=
![]() ) кездейсоқ
шамалар болсын. Сонда Стьюдент үлестiрiмi мына түрде анықталады.
) кездейсоқ
шамалар болсын. Сонда Стьюдент үлестiрiмi мына түрде анықталады.
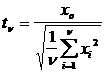
Мұнда n - еркiндiк дәрежелер саны.
Егер қалыпты үлестiрiмнiң параметрлерi а және s болса, онда xi-a кездейсоқ шамалары да тәуелсiз болады да, олардың параметрлерi сәйкес 0 және s болады. Сонда Стьюдент Үлестiрiмi төмендегiдей берiледi:
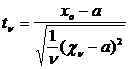
Ал a=0, s =1 болса, онда Стьюдент үлестiрiмi
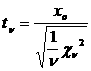
болады, мұндағы
![]() жоғарында қарастырылған
жоғарында қарастырылған
![]() үлестiрiмi.
үлестiрiмi.
3. Фишер үлестiрiмi /F - үлестiрiмi/
Айталық параметрлерi (0,s) болатын тәуелсiз қалыпты үлестiрiммен берiлген кездейсоқ шамалар қарастырылсын:
![]()
Сонда мына функция арқылы берiлген кездейсоқ шаманы Фишер үлестiрiмi арқылы берiлген деп атайды:
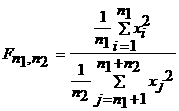
Егер xi - кездейсоқ шамалардың параметрлерi (a,s) болса, онда
Фишер үлестiрiмi төмендегiдей анықталады:
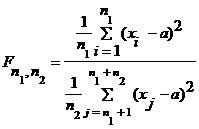
Ал егер а=0, s=1 болса, онда Фишер үлестiрiмi былай жазылады:
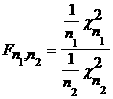
Мұндағы
![]() және
және
![]() кездейсоқ шамалары
кездейсоқ шамалары
![]() - үлестiрiммен
берiлген.
- үлестiрiммен
берiлген.
IV-блок. Үлкен сандар заңы
15-сабақ. Чебышев теңсіздігі
Үлкен сандар заңы бiрнеше теоремалар арқылы берiледi. Бұл теоремаларда (С.Чебышев, Бернулли; Пуассон теоремалары) өте көп кездейсоқ факторлардың жиынтық әсерi кездейсоқтықтан тәуелсiз нәтижелер алудың шарттары берiледi.
1 Чебышев теңсiздiгi
Егер Х кездейсоқ шамасының дисперсиясы бар болса, онда мына теңсiздiктер орындалады:
![]() (2.5.1)
(2.5.1)
![]() (2.5.2)
(2.5.2)
мұндағы
<
![]()
Бұл теңсiздiктер кездейсоқ шаманың өзiнiң математикалық үмiтiнен ауытқуын бағалайды.
Мысал 1. Дискреттi кездейсоқ шама үлестiрiм заңымен берiлген
|
Х |
-1 |
0 |
2 |
4 |
6 |
|
Р |
0,2 |
0,4 |
0,3 |
0,05 |
0,05 |
1. Мына теңсiздiктiң |x-M(x)|<5 орындалуының ықтималдығын табыңыз.
2. Чебышев теңсiздiгiн пайдаланып |x-M(x)|<5 теңсiздiгiнiң орындалуының ықтималдығын бағалаңыз.
Шешуi: Әуелi математикалық үмiт, дисперсиясын табалық.
![]()
Ендi дисперсия табу үшiн Х2 - тың үлестiрiм заңын жазамыз:
|
Х2 |
1 |
0 |
4 |
16 |
36 |
|
Р |
0,2 |
0,4 |
0,3 |
0,05 |
0,05 |
Сонда
![]()
![]()
1. Ендi |x-0,9|<5 теңсiздiгiнiң орындалу ықтималдығын табу үшiн осы теңсiздiктi қанағатандыратын Х-тiң мәндерiн анықтау қажет. Берiлген үлестiрiм кестесiмен бұл теңсiздiктi кездейсоқ шаманың x=-1, x=0, x=2, x=4 мәндерi қанағаттандыратынына көз жеткiзуге болады. Олай болса
![]()
0,2+0,4+0,3+0,05=0,95
![]()
Сонымен
![]()
2. Чебышев теңсiздiгiн пайдаланып |x-0,9|<5 теңсiздiгiнiң орындалуын бағалайық:
![]()
яғни
![]() .
.
Сөйтiп Чебышев
теңсiздiгiн пайдаланып |x-M(x)|
![]() 5
теңсiздiгiнiң орындалуының ықтималдығын
төменнен бағаладық, яғни |x-0,9|
5
теңсiздiгiнiң орындалуының ықтималдығын
төменнен бағаладық, яғни |x-0,9|
![]() 5 теңсiздiгi
кем дегенде 0,8724 ықтималдықпен орындалады. Бұл
тұжырымның құндылығы есептер шығарған кезде |x-M(x)| < e (e>0)
теңсiздiгiнiң
орындалуының дәл ықтималдығын табу мүмкiн болмаған
жағдайларда оның ықтималдығын төменнен
бағалауға мүмкiндiк бередi.
5 теңсiздiгi
кем дегенде 0,8724 ықтималдықпен орындалады. Бұл
тұжырымның құндылығы есептер шығарған кезде |x-M(x)| < e (e>0)
теңсiздiгiнiң
орындалуының дәл ықтималдығын табу мүмкiн болмаған
жағдайларда оның ықтималдығын төменнен
бағалауға мүмкiндiк бередi.
Мысал 2. Жарық берушi торға 20 электрошам параллель қосылған. Т уақыт iшiнде әрбiр шамның жарық беру ықтималдығы 0,8. Чебышев теңсiздiгiн пайдаланып Т уақытында жарық берушi барлық электрошамдармен, жарық берiп тұрған шамдардың арифметикалық орташа мәндерiнiң (математикалық үмiтi) айырмасының абсолюттiк шамасының ықтималдығын бағалаңыз. Егер айтылған айырма: 1) төрттен кiшi болса; 2) төрттен кем болмаса.
Шешуi: Белгiлi бiр Т уақытында жарық берiп тұрған электрошамдардың саны кездейсоқ шама. Бұл кездейсоқ шама биномдық үлестiрiм заңымен берiлген. Есептiң шарты бойынша n=20, p=0,8, q=0,2.
Сондықтан
M(x) = 20×0,8 = 16, D(x) = 16×0,2 = 3,2
Ендi Чебышев теңсiздiгiн пайдаланамыз
1
![]()
2
![]()
Сонымен
![]()
![]()
Мысал 3. Зауыт өнiмдерiнiң 75 процентiн жоғарғы сортпен шығарады. Шығарылған 100000 бұйымдардың iшiнде жоғарғы сортпен шығарылған бұйымдардың саны осы жоғарғы сортпен шығарылған бұйымдардың математикалық ұмiтiнен айырмасының абсолют шамасы 1000 данадан артық болмауының ықтималдығын бағалаңыз.
Шешуi: Жоғарғы сортпен шығарылған бұйымдар саны кездейсоқ шама. Оны Х арқылы белгiлейiк. Бұл кездейсоқ шама биномдық үлестiрiммен берiлген. М(х) осы кездейсоқ шаманың математикалық үмiтi. Есептiң шарты бойынша n=100000, P=0,75, q=0,25.
Сонда
М(х)=100000×0,75=75000, D(x)=18750
Осыдан
![]()
яғни
![]()
16-сабақ. Чебышев, Бернулли теоремалары
2.1 Чебышев теоремасы
Егер Х1, Х2, ..., Хn қос-қостан тәуелсiз кездейсоқ шамаларының ақырлы математикалық үмiттерi бар болып және дисперсиялары тұрақты С санымен шектелген болса, онда кез-келген n саны үшiн.
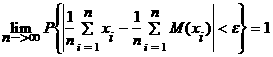 (2.1.1)
(2.1.1)
орындалады.
Бұл теореманы Чебышев теңсiздiгiн пайдаланып дәлелдегенде төмендегi бағалау алынады:
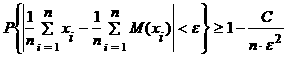 (2.1.2)
(2.1.2)
Егер М(хi)=а болса, онда (2.5.3) формула былай жазылады:
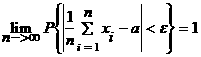 (2.1.3)
(2.1.3)
Чебышев теоремасының мағынасын түсiндiру үшiн мысал қарастырайық. Айталық белгiлi бiр бұйымның бiр өлшемi А болсын. Соны өлшеу керек. Өлшеу кезiнде әртүрлi себептерге байланысты қате кетедi. Сондықтан өлшеу кезiнде алынған нәтиже кездейсоқ шама болады. Бұл Х кездейсоқ шаманың математикалық үмiтi өлшеп отырған А шамасына тең болады, ал дисперсиясы D(x) пайдаланып отырған прибордың дәлдiгiн көрсетедi. Тәуелсiз n өлшеу жасалық.
Сонда x1, x2, ..., xn, сәйкес бiрiншi, екiншi, .... , n - шi өлшеулердiң нәтижелерi. Бұлардың өздерi кездейсоқ шамалар, олардың үлестiрiм заңдары Х-тiң үлестiрiм заңындай болады. Олай болса
![]()
кездейсоқ шамасыныңда үлестiрiм заңы сондай болады. Бiрақта n өскен сайын Х-тiң кездейсоқ сипаты бiрте-бiрте жоғала баcтайды да ол А-ға жақындай түседi. Х-тiң А-ға жақындағандығының шарттары Чебышев теоремасымен берiледi. Сонымен теореманың мағынасы:
|X-А|<e оқиғасы n мейлiнше үлкен болғанда ақиқат оқиға болады. Бұл теореманың практикалық маңызы мынада. Бiр нәрсенi өлшегенде мейлiнше дәл нәтиже алу үшiн оны бiрнеше рет өлшеп содан кейiн алған нәтижелердiң арифметикалық орташа мәнiн алу керек.
Мысал 1. Белгiлi бiр шаманың мәнi ретiнде мейлiнше көп өлшеулердiң арифметикалық орташа нәтижесi алынады. Әрбiр өлшеудiң мүмкiн мәндерiнiң орташа квадраттық ауытқуы 1 сантиметрден аспайды, деп қарастырып, 1000 өлшеуде алынған нәтиженiң берiлген шаманың шын мәнiнен ауытқуының абсолют шамасы 0,1 сантиметрден артық болмауының ықтималдығын бағалаңыз.
Шешуi: Әрбiр өлшеудiң нәтижесi кездейсоқ шама болады. Сондықтан 1000 өлшеудiң нәтижелерiн x1, x2, ..., x1000
тәуелсiз кездейсоқ шамалар жиынтығы ретiнде қарастырамыз. Сонда
![]()
100 өлшеудiң арифметикалық орташа мәнi болады. Ол да кездейсоқ шама болады. Ендi өлшеп отырған шаманың шын мәнiн а деп қабылдасақ. Чебышев теоремасын пайдалануға болады:
![]()
Cөйтiп
![]()
Мысал 2. Электрошамдар салынған 100 жәшiктiң әрқайсысынан олардың жану ұзақтығын анықтау үшiн бiр-бiрден электрошам алынды. Сөйтiп алынған шамдардың жану ұзақтығының арифметикалық орташа жану ұзақтығы есептелiндi. Осы арифметикалық орташа жану ұзақтығының жәшiктердегi барлық шамдардың жану ұзақтығының арифметикалық орташа жану ұзақтығынан айырмасының абсолют шамасының 2 сағаттан көп болмауының ықтималдығын бағалау керек. Шамдардың жану ұзақтығының орташа квадраттық ауытқуы 8 сағаттан аспайды.
Шешуi: Кездейсоқ шамаларға белгiлеу енгiзелiк. Хi i-iншi жәшiктен алынған электрошамның жану ұзақтығы, М(хi) - әр жәшiктегi шамдардың арифметикалық орташа жану ұзақтығы. Сонда
![]()
алынған шамдардың арифметикалық орташа жану ұзақтығы, ал
![]()
барлық шамдардың жану ұзақтығының арифметикалық орташа жану ұзақтығы. Сонымен есептiң шарты бойынша мына ықтималдықты бағалау керек.
![]()
Қарастырып отырған x1, x2, ..., x100 кездейсоқ шамалар үшiн Чебышев теоремасының шарттары орындалады. Олай болса
![]()
Сөйтiп
![]()
Mысал 3. Белгiлi бiр шаманы өлшегенде алынған нәтижелер дисперсиясы 1-ден аспайтын кездейсоқ шама. Осы нәтижелердiң арифметикалық орташа мәнiнiң берiлген шаманың шын мәнiн ауытқуының абсолют шамасы 0,01-ден артпауының ықтималдығы 0,98 - ден кем болмауы үшiн қанша өлшеу керек?
Шешуi: Әрбiр өлшеу кезiнде алынған нәтижелер кездейсоқ шама және олар тәуелсiз. Белгiлеу енгiзелiк
x1, x2, ..., xn
бiрiншi, екiншi, ... , n-шi өлшеулердiң нәтижелерi. Олай болса олардың арифметикалық орташа мәнi де
![]()
кездейсоқ шама. Ендi өлшеп отырған шаманың шын мәнiн а - деп белгiлесек, сонда бұл кездейсоқ шамалар Чебышев теоремасының шарттарын қанағаттандырады. Сондықтан
![]() .
.
Oсыдан мына теңсiздiктi аламыз:
![]()
Соңғы теңсiздiктi
шешiп
![]() болатынын көремiз.
болатынын көремiз.
Мысал 4. Егер тәуелсiз x1, x2, ..., xn кездейсоқ шамалар тiзбегi төмендегiдей үлестiрiм заңымен берiлсе
|
Xn |
-3n |
0 |
3n |
|
P |
|
|
|
онда осы кездейсоқ шамалар тiзбегiне Чебышев теоремасын қолдануға бола ма?
Шешуi: Берiлген кездейсоқ шамалар тiзбегiне Чебышев теоремасын пайдалану үшiн бұл тiзбектер екi шартты қанағаттандыру керек:
1)Олар қос-қостан тәуелсiз болу керек.
2)Олардың математикалық үмiттерi ақырлы болып, дисперсиялары тұрақты бiр С санымен шектелген болуы керек.
Берiлген кездейсоқ шамалар үшiн бiрiншi шарт орындалады, себебi есептiң шарты бойынша олар тәуелсiз кездейсоқ шамалар. Ал екiншi шарттың орындалуын тексеру қажет. Әуелi математикалық үмiттердi есептейiк:
M(xn) = -
![]() +
+
![]() =0
=0
Ендi хn2 үшiн үлестiрiм кестесiн жазайық.
|
Хn2 |
9n2 |
0 |
9n2 |
|
P |
|
|
|
Осыдан
М(хn2) =
![]()
ақырында D(x)=
![]()
Cонымен М(хn) ақырлы болады да, ал D(xn) шектелген болады. Олай болса Чебышев теоремасын пайдалануға болады.
2.2 Бернулли теоремасы
Егер әрбiр тәуелсiз n сынақтарда А оқиғасы тұрақты р ықтималдықпен m рет пайда болса, онда кез-келген n үшiн
![]() (2.2.1)
(2.2.1)
орындалады.
Бұл теореманы Чебышев теңсiздiгiн пайдаланып дәлелдегенде төмендегi бағалауды аламыз:
![]() (2.2,2)
(2.2,2)
Мысал 5. Оқиға тәуелсiз сынақтарда тұрақты 0,2 ықтималдықпен пайда болады. Оқиғаның 900 сынақтарда пайда болу салыстырмалы жиiлiгiнiң осы оқиғаның ықтималдығынан ауытқуының абсолют шамасы 0,04-ден кем болатындығының ықтималдығын бағалаңыз.
Шешуi: Есептiң шарттары Бернулли теоремасының шаттарымен сәйкес келедi. Сондықтан n=900, р=0,2, q=0,8, e=0,04 екенiн ескерiп, iздеп отырған ықтималдықты бағалау үшiн (2.5.7) формуланы пайдаланамыз.
![]()
Осыдан
![]()
Mысал 6. А оқиғасының тәжiрибеде пайда болу ықтималдығы 0,75-ке тең. Осы тәжiрибелерде оқиғаның пайда болуы салыстырмалы жиiлiгiнiң оның ықтималдығынан ауытқуының абсолют шамасы 0,05-тен артық болмауының ықтималдығы 0,96-ға тең болу үшiн қанша тәжiрибе жасау керек?
Шешуi: Есептiң шарты бойынша
![]()
(2.5.7) формуладан
-
![]()
Осыдан n³1875.
Мысал 7. Зауыт дайындалған бұйымның 90 процентi бiрiншi сортқа
жатады. Тексеруге 600 бұйым алынды. Тексеруге алынған бұйымдардың iшiндегi бiрiншi сортқа жататын бұйымдардың үлесiнiң оның ықтималдығынан ауытқуының абсолют шамасы
![]() -нен кем болуының ықтималдығы
0,99-ға тең болуы
үшiн бұл ауытқу қандай болуы керек?
-нен кем болуының ықтималдығы
0,99-ға тең болуы
үшiн бұл ауытқу қандай болуы керек?
Шешуi: Есептiң шартын пайдалансақ онда мына теңдiктi жазамыз
![]()
Осыдан
-
![]() ,
,
немесе e=0,12.
ЖАТТЫҒУ Е С Е П Т Е РІ
1. Екi атқыш нысанаға бiр-бiрден атыс жасады. Нысанаға тигiзу ықтималдығы бiрiншi атқыш үшiн 0,6 ал екiншiсiнiкi - 0,8. Кездейсоқ шама Х-нысанаға тигiзудiң саны. Осы кездейсоқ шаманың үлестiрiм кестесiн құрыңыз.
2. Нысанаға тигiзу ықтималдығы 2/3 тең. Үш атыс жасағанда нысанаға тию санының үлестiрiм кестесiн құрыңыз.
..